Dessiner la fonction zeta sur le plan complexe requiert quelques manipulations mathématiques et informatiques. On va pour cela utiliser l'équation fonctionnelle et ainsi prolonger la fonction hors de son demi-plan de définition.

1) Fonction Gamma

Dans cette section on tracera les graphes sur les pavés [-7,7] + i [-7,7] sauf mention du contraire.

On aura besoin de la fonction Gamma sur 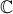pour pouvoir définir zeta avec l'équation fonctionnelle. À priori Gamma est définie par l'équation 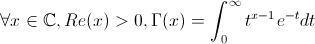     Sur le demi plan de droite, on a : 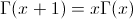  . Pour tracer la fonction gamma sur le plan, on pourrait travailler avec la formule intégrale, mais on va utiliser une propriété (non triviale) de cette fonction : 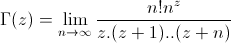   qui est plus commode pour programmer (et qui a le mérite d'être valable sur ).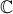

Finalement cela donne le graphe suivant la fonction Gamma :
                        

     On peut remarquer une croissance forte (du module) en direction des parties réelles croissantes. La fonction a des pôles sur les entiers négatifs. Les pôles sont simples et de résidus très décroissants (en 1/n!). On peut voir que la droite réelle est stabilisée (là où la fonction est définie). La fonction Gamma est facile à tracer, et indispensable pour définir la fonction zeta sur tout le plan.
   Une propriété notable : la fonction Gamma ne s'annulant pas sur le plan, son inverse est holomorphe sur 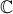. On peut donc regarder sa singularité à l'infini non ? (voir  Singularités pour d'autres singularités à l'infini !)

La fonction 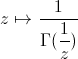sur [ -0.3 , 0.3 ] + i [ -0.3 , 0.3 ] :
 
   
     Nice n'est ce pas ? À droite de 0, la noirceur des points témoigne de l'explosion du module de Gamma car son inverse est très faible. De l'autre côté une suite de zéros de la fonction converge vers 0. Ils sont de plus en plus discrets à l'approche de l'origine.
    La valeur de cette image est à ne pas surestimer, c'est un des dessins pour lesquel j'ai le moins de méthodes te tests de validité. J'ai du mal à calculer l'équivalent de l'erreur dans mon approximation de Gamma donc la "vraie" singularité de Gamma n'a peut-être pas exactement cette dégaine... Mais si je l'ai mise ici c'est quand même que je pense qu'elle est, au moins, pas loin d'être juste.


2) Fonction Zeta

   À priori la fonction zeta est donnée par la somme 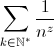  ou le produit 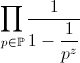. Pour chacun des deux la convergence a lieu dans le demi-plan { Re(z) > 1 }. Cette fonction a pourtant un prolongement sur le plan complexe, on imagine alors qu'elle aura une singularité sur la droite de partie réelle 1. Mais en fait on peut aller plus loin que 1 grâce à la fonction 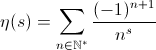, qui converge jusqu'à zéro. Une relation lian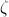t  et 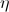permet alors de calculer 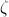sur, par exemple, [ 0.5 , 3.5 ] + i [ -1.5 , 1.5 ] :
                                                   

   On peut la tracer sur tout le demi-plan de droite, à partir de 0. Par ailleurs sur la bande   {0< Re(z)<1}, la fonction zeta vérifie une équation fonctionnelle. Comme elle est vérifiée sur un ouvert elle l'est sur :
                                               
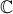  Donc en connaissant le sinus, Gamma, et zeta sur le demi plan de droite, on peut la prolonger informatiquement  :

Fonction zeta sur le carré [-7,7] + i [-7,7] :
                     

       On voit apparaître le pôle en 1 ainsi que des zéros "triviaux" de la fonction zeta, aux points pairs négatifs (-2,-4,-6). À droite, la fonction est très ressemblante à une fonction constante car elle est très proche de 1 dès que la partie réelle du nombre évalué est grande. Les bandes verticales viennent de la limite de calcul de mon ordinateur, je ne peux pas aller assez loin dans les sommes qui définissent mes fonctions.

   Et Bob se dit peut-être, "mais où sont les fameux zéros non triviaux de la fonction zeta" ? Sur la droite de partie réelle 1/2 assurément ! et on peut en voir quelques uns en regardant la fonction de plus loin :

Fonction zeta sur [-50,10] + i [-30,30] :
 


        Et voici presque 8 zéros non triviaux de la fonction. La bande de discontinuité apparente est à nouveau due à la limite de la puissance informatique de mon ordinateur, je ne peux pas demander un meilleur résultat dans un temps raisonnable.

Mais au fait, cette fonction est holomorphe sur , on doit pouvoir regarder sa singularité à l'infini non ? Eh oui !

La fonction 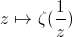sur [ -0.3 , 0.3 ] + i [ -0.3 , 0.3 ] :
                         

    Nice aussi, on ne voit plus le pôle (car on regarde de trop près).
Et, en y réfléchissant très fort ...
(ce qui signifie, avec un papier et un stylo pour les mathématicien(ne)s),...
(on peut s'aider de la dernière image de la page Fonctions modulaires si on le souhaite, celle avec les domaines fondamentaux !),
... La suite de zéros de la fonction qu'on voit plonger de façon verticale sur 0, n'est autre que l'ensemble des zéros non triviaux de la fonction zeta ! De plus, la conjecture de Riemann revient à voir que sur ce dessin, ils sont tous cocentriques ! ça ne saute pas aux yeux ici (sinon j'aurais déjà gagné le million de dollars !). D'ailleurs mon dessin ne le vérifie probablement pas à cause de tous les facteurs d'erreur de mes programmes.
Pour voir d'autres singularités à l'infini plongées dans le plan, voir Page d'accueil, Homographies ou Singularités !



   La suite ne vous intéressera que si vous souhaitez programmer 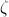 sur votre ordinateur, ou si vous savez le faire mieux que moi !

4) Bilan des difficultés informatiques

   En fait les principales difficultés informatiques viennent de problèmes de convergence. Par exemple, la présence du pôle en 1 de la fonction se voit grâce à la divergence de . La somme partielle de cette série équivaut à Ln(N). Cela pose un problème informatique majeur : pour dépasser 100, il faut additionner exp(100) termes dans la série, bien au delà des possibilités d'un ordinateur.

   Pour faire apparaître le pôle, il faut ruser en utilisant une série ALTERNEE des termes de  :
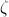   Comme cette série converge sur l'ensemble {Re(z)>0} qui contient strictement le pôle de , on peut sommer jusqu'à 1 avec une convergence acceptable. Ensuite une relation simple lie  et son copain alterné, 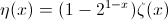   ce qui permet de tracer 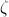sur un voisinage de 1.

   Mais ça suffit à peine à la prolonger sur 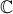: la relation fonctionnelle de 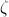est symétrique par rapport à 1. On a donc besoin de connaître  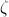jusqu'à  {Re(z)=1/2} (à méditer, mais   min( max(x,1-x)) =0.5  ). C'est théoriquement possible car 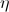converge jusqu'à 0. , Mais ça requiert de sommer la fonction au pire jusqu'à 1/2 où le problème de convergence se pose le plus. Le terme général décroît alors en 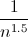 en module, ce qui donne une convergence en 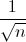de la somme partielle, ce qui est assez nazzzze !
(en fait, on associe les termes consécutifs deux à deux dans la somme, ce sont les "paires de termes" de 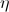 qui vérifient ces propriétés)

Aux points les plus proches de 0.5 j'ai programmé une somme jusqu'à 50 000 termes de la suite afin d'avoir un terme général assez faible pour être raisonnable... Ca ne permet que d'avoir une approximation des valeurs de l'ordre du centième, parfois pire.
   On pourrait essayer de trouver un équivalent du reste partiel au rang N pour pouvoir améliorer ça, mais en essayant, j'ai maintes fois échoué, jusqu'à admettre que je n'y parviendrai pas.

Si un éventuel lecteur a une suggestion à faire pour contourner cette difficulté de convergence ou exprimer cet équivalent, je suis preneur. Pour m'envoyer un mail, mon adresse est :  merci d'avance !