1) Fonction logarithme

    Comme on le sait peut-être, il n'existe pas de logarithme continu sur , il faut enlever une demi-droite de discontinuité. En fait on peut enlever n'importe quelle courbe reliant 0 à l'infini. On peut illustrer ça avec des changements de cartes projectifs :

                               Log sur [-5,5]+ i [-5,5]                                          Log( 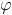) sur [ -1.5 , 1.5 ] + i [ -1.5 , 1.5 ]
                           

        On prend le changement de carte 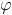 défini par 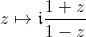. On voit alors que les points 0 et l'infini ont un rôle symétrique dans la discontinuité. Il s'agit juste d'une courbe injective reliant les deux points.

  (Pour mieux comprendre ces représentations, on peut lire   4)Bijections de l'espace projectif sur la page Homographies ! C'est une partie plutôt accessible, dans laquelle ce même changement de variable est illustré)

Du côté où la discontinuité est un cercle (ci-dessus à droite), on peut déformer cette discontinuité (ci-dessous à gauche), puis la renvoyer à son domaine initial (ci-dessous à droite) :

                Log2 ( 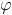) sur [ -1.5 , 1.5 ] + i [ -1.5 , 1.5 ]                                         Log2 sur [-5,5]+ i [-5,5]    
                            

       On peut ainsi imaginer beaucoup de façons de déformer la droite de discontinuités pour obtenir autant de logarithmes. Bien sûr, il faut avoir une façon de déterminer le logarithme au delà de la discontinuité, mais c'est en fait facile : la discontinuité du log est de 2i 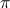à la traversée de la discontinuité ; il suffit de les ajouter et on prolonge le logarithme initial.
   N'importe quelle courbe     continue telle que 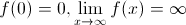 et  injective (sans points doubles) et qui n'intersecte pas 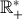 définit un logarithme qui pronlonge le logarithme réel : c'est la courbe de discontinuité  du Logarithme.

 Si on veut juste prolonger le germe du Log en 1, la courbe de discontinuité doit seulement éviter 1 (et pas )

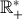                Log3 ( 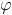) sur [ -1.5 , 1.5 ] + i [ -1.5 , 1.5 ]                                         Log3 sur [-5,5]+ i [-5,5]    
                            

      Celui là ne prolonge pas le logarithme de 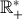(il y a des points entre 0 et 1 par lesquels passe la courbe) mais il reste possible à construire depuis le germe du logartihme principal en 1. Pour en savoir plus sur les germes RDV sur la page Séries entières !
 
2) La rotation du logarithme

   Si on veut juste une réciproque de l'exponentielle, il suffit de définir une courbe injective reliant 0 à l'infini (on n'impose plus de valeur en 1 à la fonction) et un germe de logarithme en un point. En pratique, on choisit un k dans Z, et on ajoute 2i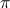k au logarithme principal. En pratique, autant partir du logarithme principal, sauf dans le contexte suivant :

Toute demi-droite partant de 0 définit une courbe de discontinuité du logarithme. On va faire tourner la demi-droite :
Le rectangle de traçage est [-2,2] + i [-2,2]   

                                                    
                         

                                          
                       

   Après un tour complet, déjà on remarque qu'il n'y a plus rien en commun avec la fonction de départ : elle a été "translatée" de 2i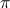. Cette fonction ne prolonge aucun germe du logartithme principal. On pourrait continuer à faire tourner la droite (et dans l'autre direction aussi) et on obtiendrait ainsi TOUS les germes de logarithmes (au sens local), mais pas toutes les fonctions logarithmes, ne serait-ce que parcequ'on en a trouvé d'autres types en début de page.

Pour encore plus de germes du logarithme, RDV sur la page Séries entières !

3) La rotation de la racine carrée

    Et Bob se demande : "que se passe t-il en faisant la rotation la racine carrée ?" C'est une excellente question Bob, on pourrait imaginer un comportement similaire, et... (Voir plus haut "rotation du logarithme" pour les détails) .. y'a des choses qui diffèrent...

On va déterminer des racines carrées différentes en changeant la définition du logarithmme. Pour ça on fait tourner une droite de discontinuité autour de 0, et on observe ce qui se passe après plusieurs tours :

On part du Logarithme principal et de la première racine carrée :   et  =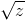
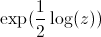
Puis on fait tourner le logarithme d'un angle  à chaque étape :

                        Racine 0                                                        Racine 1                                                      Racine 2
              
Ah et on tourne dans l'autre sens aussi (des aiguilles d'une montre)...   Et le carré est toujours [-2,2] + i [-2,2]
Encore un tour....
                     Racine 3                                                              Racine 4                                                     Racine 5
             


   ...  et on retombe sur la racine initiale. Pourquoi ? car  le logarithme s'est décalé de 4i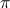, donc la racine  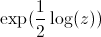est multipliée par 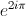=1 : elle  est inchangée ! On peut l'illustrer avec ce GIF qui est peut-être plus parlant (et qui tourne dans le bon sens) :

                                                 

    Pour une racine n-ième, de la même façon, on retombe sur la détermination initiale après n tours.
Voila ce qui se passe quand on prolonge un germe de fonction analytique autour d'une singularité. Parfois tout du moins ; Certains germes déterminent une fonction sur un ensemble "avec un trou". Un exemple est illustré dans la page Séries entières !
D'autres fonctions multiformes sont aussi présentées sur la page Fonctions principales !

3) Logarithmes et arc-sinus

    On se rappelle que l'arc sinus pronlongeant celui d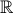e ne peut pas être continu en -1 ou 1. Il a deux demi-droites de discontinuités (voir Fonctions principales si vous n'en êtes pas convaincu).  Il est déterminé par le choix d'une racine et d'un logarithme.
Voici le logarithme exprimé dans une carte projective qui laisse 1 et -1 invariants, et qui ramène l'infini en i :

Logarithme principal sur 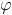([-2,2] + i [-2,2]) :
                       

Un logarithme quoi, il a une courbe de discontinuité qui relie 0 à l'infini ! Si vous voulez mieux comprendre ces cartes projectives, voir la page Homographies !
 
Arc-sinus principal sur 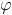([-2,2] + i [-2,2]) :
                     

    On remarque que les deux discontinuités se rejoignent parfaitement à l'infini, malgré un choix très arbitraire de logartithmes et de racines. La "singularité" en 1 de l'arc-sinus joue le même rôle de détermination que la "singularité" à l'infini du logartithme.

   Par contre, on voit que la discontinuité de l'arcsinus doit impérativement relier 1 à l'infini et -1 à l'infini. Elle a plus de contraintes que la courbe de discontinuités d'un logarithme.