1) Fonctions méromorphes
Qu'est ce qu'une fonction méromorphe ? On peut la penser comme le quotient de deux fonctions holomorphes, il se trouve que le théorème de factorisation de Weierstrass permet de l'affirmer. Le niveau 1 des fonctions méromorphes du coup ce sont les fractions rationnelles :
La fraction rationnelle :
 sur le carré [-2,2] + i [ -1.5 , 2.5 ]
sur le carré [-2,2] + i [ -1.5 , 2.5 ]
On peut bien distinguer l'ordre (fini) des zéros et des pôles. Les fractions rationnelles n'ont qu'un nombre fini de singularités et zéros. On voit bien que le module tend vers l'infini au voisinage des pôles, et vers 0 au voisinage des zéros. Cela distingue les pôles/zéros des singularités essentielles.
Petit rappel : les zéros sont les points affichés en NOIR, les pôles en BLANC
l'ordre d'un zéro/pôle est le nombre de tours que fait la teinte autour du point.
Une fonction méromorphe :
 sur [-2,2] + i [-2,2]
sur [-2,2] + i [-2,2]
Elle a des zéros et des pôles dans 4 direction, en nombre infini. Ils sont tous d'ordre 1, sauf en plein centre (0) où le zéro est d'ordre 4.
La fonction
 de Weierstrass
avec le groupe de périodes
de Weierstrass
avec le groupe de périodes  tracée sur [ -1.5 , 1.5 ] + i [ -1.5 , 1.5 ]:
tracée sur [ -1.5 , 1.5 ] + i [ -1.5 , 1.5 ]:

C'est une fonction avec une double période (1 et i ), donc toutes les combinaisons
 -linéaires de 1 et i sont des périodes. Le groupe de période est ici
-linéaires de 1 et i sont des périodes. Le groupe de période est ici  [i]. Pour chaque couple
de complexes non colinéaires,
il existe une fonction
[i]. Pour chaque couple
de complexes non colinéaires,
il existe une fonction  qui admet
ces deux nombres comme période. Par ailleurs
qui admet
ces deux nombres comme période. Par ailleurs  et sa dérivée engendrent le corps des fonctions
méromorphes sur le tore quotient défini par les deux nombres.
Une construction possible des fonctions modulaires (et notamment de la
fonction J) est basée sur cette fonction. On isole un invariant de
réseau grâce à
et sa dérivée engendrent le corps des fonctions
méromorphes sur le tore quotient défini par les deux nombres.
Une construction possible des fonctions modulaires (et notamment de la
fonction J) est basée sur cette fonction. On isole un invariant de
réseau grâce à  puis on
définit une fonction de réseau, qui engendre une fonction modulaire.
puis on
définit une fonction de réseau, qui engendre une fonction modulaire.
Il est assez intéressant aussi de se demander quelles sont les deux fonctions holomorphes sur
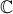 dont
dont  est le quotient. La réponse est non triviale...
est le quotient. La réponse est non triviale...Par ailleurs deux paires de nombres complexes non
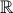 colinéaires
peuvent définir le même réseau. Voici un GIF pour l'illustrer
:
on représente les fonctions de Weierstrass des réseaux variant de (1,i)
à (1, 1+i), qui sont alors les mêmes car les réseaux sont les mêmes :
colinéaires
peuvent définir le même réseau. Voici un GIF pour l'illustrer
:
on représente les fonctions de Weierstrass des réseaux variant de (1,i)
à (1, 1+i), qui sont alors les mêmes car les réseaux sont les mêmes : 
La fonction
 a beaucoup à voir avec
les définitions des fonctions modulaires, mais je le détaille pas.
Malgré tout, vous reconnaîtrez peut-être ces symétries de réseaux en
allant voir la page Fonctions
modulaires !
a beaucoup à voir avec
les définitions des fonctions modulaires, mais je le détaille pas.
Malgré tout, vous reconnaîtrez peut-être ces symétries de réseaux en
allant voir la page Fonctions
modulaires !Un dernier mot sur la fonction de Weierstrass : il n'est pas intéressant sur le plan mathématique de la regarder à l'infini : on la connaît partout dès qu'on la connaît sur le carré [0,1] + i [0,1]. Mais on imagine bien que ça peut être joli de replier le réseau
 [i] !
[i] !Donc voici la fonction
 sur [-2,2] + i [-2,2]
sur [-2,2] + i [-2,2]
Bon, on voit (encore plus qu'avant) un défaut de l'image sous cet angle : les zéros devraient probablement être tous double, alors qu'ici ils le sont pas exactement. Comme mentionné plus haut, l'intérêt est plus esthétique que mathématique....
Plus bas, sur cette même page, on explique un peu mieux ce changement de carte.
2) Singularités essentielles
On l'a dit précédemment, les zéros des fonctions holomorphes non constantes ne peuvent pas être de multiplicité infinie. Ce n'est pas le cas dans
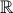 ,
et un contre-exemple classique en est la
fonction
,
et un contre-exemple classique en est la
fonction  ,
qui se prolonge en 0 par 0. Elle est infiniment dérivable, toutes ses
dérivées sont nulles en 0, mais elle n'est pas constante.
,
qui se prolonge en 0 par 0. Elle est infiniment dérivable, toutes ses
dérivées sont nulles en 0, mais elle n'est pas constante. Voici son graphe sur
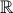 .
(tracée sur MAFA Traceur de courbes, si un jour vous voulez tracer une fonction réelle)
.
(tracée sur MAFA Traceur de courbes, si un jour vous voulez tracer une fonction réelle)
Le choix de cette fonction n'a rien d'hasardeux : la fonction
 définie
sur
définie
sur  admet une singularité essentielle en 0. Dans la direction réelle, elle
est prolongeable en 0, mais pas dans la direction imaginaire pure par
exemple.
admet une singularité essentielle en 0. Dans la direction réelle, elle
est prolongeable en 0, mais pas dans la direction imaginaire pure par
exemple.Voici son tracé sur [-1,1] + i [-1,1] :

On voit que le module tend vers l'infini en se rapprochant de 0 dans la direction imaginaire, elle n'est donc pas continue en 0.
Pour trouver une singularité essentielle, rien de plus simple : on prend une fonction entière non polynômiale genre
 , on la compose avec la fonction
inverse,
, on la compose avec la fonction
inverse,  . Comme f a une singularité
essentielle à l'infini (car elle
est non polynômiale), en faisant cette opération, on transporte sa
singularité en 0. Voilà ainsi le graphe de
. Comme f a une singularité
essentielle à l'infini (car elle
est non polynômiale), en faisant cette opération, on transporte sa
singularité en 0. Voilà ainsi le graphe de  sur [ -0.5 , 0.5 ]
+ i [ -0.5 , 0.5 ], avec une belle singularité en 0 :
sur [ -0.5 , 0.5 ]
+ i [ -0.5 , 0.5 ], avec une belle singularité en 0 :
Pour mieux voir le lien entre le graphe d'une fonction et son graphe à l'infini, RDV sur Homographies ou Fonction zeta, où vous trouverez des fonctions exprimées dans les deux cartes. (ou plus haut sur cette page, avec la fonction
 )
)Les singularités essentielles ont des propriétés épatantes : par exemple, il est facile de voir que l'image de tout voisinage épointé de la singularité est dense et ouvert dans
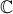 .
On peut de plus affirmer d'après le théorème de Picard, que la fonction
restreinte à un voisinage épointé est surjective sur
.
On peut de plus affirmer d'après le théorème de Picard, que la fonction
restreinte à un voisinage épointé est surjective sur 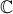 ou presque : elle ne
peut éviter qu'un point.
ou presque : elle ne
peut éviter qu'un point. C'est le cas de cette dernière singularité, la plus immédiate à imaginer :
 sur le
carré [ -0.5 , 0.5 ] + i [ -0.5 , 0.5 ] :
sur le
carré [ -0.5 , 0.5 ] + i [ -0.5 , 0.5 ] :
C'est la première fonction "difficile" que Thomas Schmitt et moi avons laborieusement fini par tracer, sans librairie complexe, et sa réalisation nous a pris une nuit de modifications sur le code. C'est ce jour là que nous avons imaginé toutes les ruses nécessaires pour faire ces illustrations informatiques. Elles sont détaillées sur la page Mode de représentation !
Les courbes d'équimodule et d'équi argument forment des cercles passant tous par zéro : cela rappelle les lignes de champ et les lignes d'équipotentielles d'un dipôle electrostatique, qui avaient parfois cette même propriété. De plus de la même façon, les lignes de champs et d'équipotentielles sont orthogonales (à cause de grad(V)=0 sur les équipotentielles, et le fait que le gradient dirige les lignes de champ) donc ils doivent avoir un peu la même dégaine j'imagine, bien qu'on ne les représente pas avec tant de couleurs.
Par rapport à ce qu'on a vu sur le théorème de Picard, cette singularité là rate toujours un point : il n'y a pas de complexe dont l'exponentielle est nulle. Donc
 est
surjective sur
est
surjective sur  ,
même si on la restreint à n'importe quel voisinage épointé de 0.
,
même si on la restreint à n'importe quel voisinage épointé de 0.Une dernière singularité, d'ordre infini celle ci :
 ramenée à zéro par
l'homographie précédente : sur [ -0.5 , 0.5 ] + i [ -0.5 , 0.5]
ramenée à zéro par
l'homographie précédente : sur [ -0.5 , 0.5 ] + i [ -0.5 , 0.5]
Et voici une belle singularité essentielle et d'ordre infini ! Vous pouvez revoir plier l'infini dans Homographies, Fonction zeta, Fonctions modulaires, et dans Déterminations ! J'aime plier l'infini...