Fonctions modulaires
Cette page vient compléter plusieurs points évoqués à divers endroits sur la page Homographies, et présenter un dernier type de fonctions : les fonctions modulaires. Pour voir plus de détails mathématiques, vous êtes au mauvais endroit...
Le mieux est probablement de prendre un bouquin, il y en a un de J.P. Serre et un de R. Godement (et certainement beaucoup d'autres !) qui sont bien expliqués.
En fin de page (partie 4), il y a quelques explications et une illustration sur le groupe modulaire.
1) Séries d'Eisenstein
Les fonctions modulaires les plus simples à tracer et les plus immédiates à introduire sont les séries d'Eisenstein : on les appelle Gk ou Ek ou E2k... Ce sont des formes modulaires de poids 2k (c'est difficile à distinguer sur dessin) :
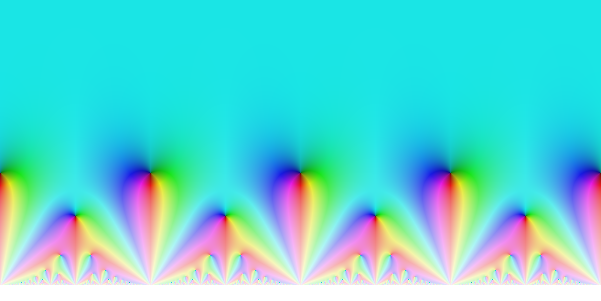
Fonction G2 tracée sur [-2,2] + i [0,2] :

Pour la définir formellement, bon courage... Elle est 1-périodique (comme toutes les fonctions modulaires) et cela permet de la représenter dans le disque D(0,1) avec le changement de variable
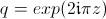 et on regarde la fonction comme une fonction de q.
et on regarde la fonction comme une fonction de q.Fonction G2 : sur [ -1.1 , 1.1 ] + i [ -1.1 , 1.1 ] :

Avec quelques problèmes de convergence sur le bord du disque : la véritable fonction est plus lisse que ça mais je n'ai pas pu la tracer plus précisément, faute de moyens informatiques. On remarque tout de même que la fonction est holomorphe à l'infini (le centre du disque) et réelle sur les axes verticaux portés par 1/2 et 1... Les images sont très claires (et un peu assombries artificiellement, je l'avoue) car les valeurs sont assez grandes en module un peu partout.
Le changement de variable est mieux expliqué plus bas sur cette page (en partie 3)
On peut aussi tracer la fonction G3 des deux mêmes façons :
Et sur le disque après le changement de variable :
Cette fonction est de poids 6. On pourrait croire qu'elle s'annule à l'infini mais non, ni aucune des séries d'Eisenstein.
2) Delta et J
La fonction
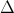 s'exprime comme un produit infini de la variable
s'exprime comme un produit infini de la variable
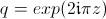 :
:
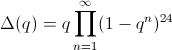 On le
multiplie encore par une constante dans certains cas. On l'appelle aussi le discriminant.
On le
multiplie encore par une constante dans certains cas. On l'appelle aussi le discriminant.La fonction Discriminant modulaire sur le rectangle [-2,2] + i [0,2] :

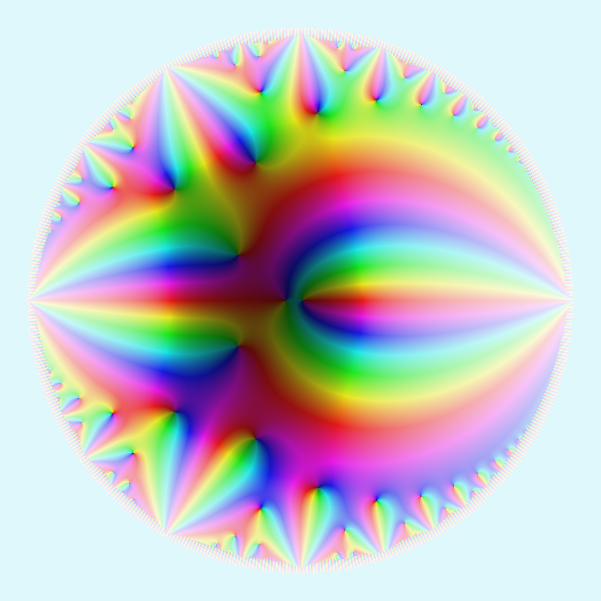
Et à nouveau, pour voir sa dégaine à l'infini, on peut regarder ce que donne la fonction sur le disque :

Là par exemple on peut voir que c'est une forme parabolique, elle s'annule à l'infini (au milieu du disque). Il s'agit d'une fonction modulaire de poids 12, qui peut s'exprimer (avec les bonnes constantes multiplicatives)
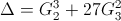 . Sans entrer dans les détails, on peut utiliser la
fonction
. Sans entrer dans les détails, on peut utiliser la
fonction  de
Weierstrass pour prouver qu'elle ne s'annule pas sur
de
Weierstrass pour prouver qu'elle ne s'annule pas sur 
 , puis définir J ainsi :
, puis définir J ainsi : 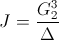 (avec des constantes et les bonnes définitions
pour les
séries d'Eisenstein). La fonction J a une propriété sympa :
elle
est de poids 0, donc l'image d'un point ne dépend que de son orbite
sous l'action de
(avec des constantes et les bonnes définitions
pour les
séries d'Eisenstein). La fonction J a une propriété sympa :
elle
est de poids 0, donc l'image d'un point ne dépend que de son orbite
sous l'action de 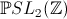 .
.
Pour toute homographie h de
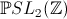 , pour tout z
dans
, pour tout z
dans  , J(h(z))=J(z)
, J(h(z))=J(z)La fonction J dessinée sur [-2,2] + i [-2,2]:
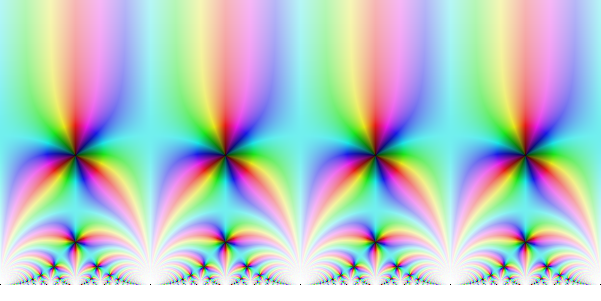
En regardant très attentivement on peut reconnaître les domaines fondamentaux les plus balaises (voir partie 4) dans la distribution des valeurs de J. Cela traduit le fait qu'elle est invariante par composition avec une homographie.
Pour l'observer à l'infini, on plie les domaines fondamentaux :

En théorie, celle ci a un pôle à l'infini, bien qu'il ne soit pas visible sur mon dessin. Donc ce n'est pas une fonction modulaire, mais presque. Les sommes des séries d'Eisenstein sont difficiles à exprimer informatiquement.
Si un éventuel lecteur a une suggestion pour tracer efficacement ces fonctions (sans passer par les séries), je suis preneur. Mon adresse mail est
 , merci d'avance !
, merci d'avance !Et pour finir un dessin perturbant sorti d'une tentative de tracer J, que j'ai appelé le cri modulaire :

La suite ne contient presque pas d'illlustration et explique quelques points mathématiques sur ces fonctions.
3) Le changement de variables
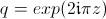
Ce changement de variable envoie le demi-plan de Poincarré vers D(0,1), mais il n'est injectif que sur les demi-bandes verticales d'épaisseur 1. Il ne s'agit donc pas d'un changement de variable holomorphe de
 vers D(0,1) !
vers D(0,1) !En fait, il réalise une bijection holomorphe de
 vers
vers 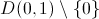 ,
et zéro devient le point à l'infini. Si on représente une fonction de
,
et zéro devient le point à l'infini. Si on représente une fonction de 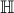 quelconque dans le disque unité, elle aura souvent un segment de discontinuité sur le disque (le segment [0,1]).
quelconque dans le disque unité, elle aura souvent un segment de discontinuité sur le disque (le segment [0,1]).Il faut s'assurer que la fonction qu'on représente est 1-périodique (ce qui est le cas pour les fonctions modulaires) et alors on peut la représenter dans le disque sans perdre d'information. Mieux : on gagne de l'information sur le comportement en 0 dans le disque, et c'est ainsi qu'on définit une autre propriété que doit nécessairement vérifier une fonction modulaire : être holomorphe à l'infini.
Cette propriété a peu de sens dans
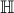 mais elle en a dans D(0,1).
mais elle en a dans D(0,1).Finalement, dans le disque, l'infini est le centre du cercle 0.
0 correspond au point 1 le plus à droite du cercle
1/2 correspond au point -1 le plus à gauche du cercle
1 correspond au point 1 du cercle
Le même point 1 du cercle décrit 0, 1, 2, -1.. Il décrit tout
 , ce qui traduit la bijection avec le quotient
, ce qui traduit la bijection avec le quotient 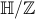 .
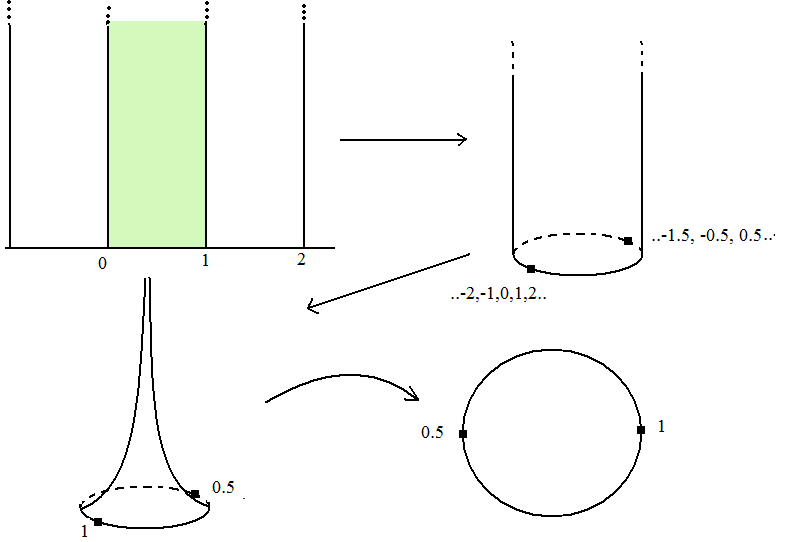
.Si Bob veut imaginer l'allure de ce changement de variable (à méditer profondément, avec un stylo si possible) :
- on part d'une demi bande infinie { z , 0<Re(z)<1 , Im(z)>0} d'épaisseur 1, vers le haut
- on colle les deux bords infinis (c'est le quotient par
 ) pour se retrouver avec demi-cylindre infini
) pour se retrouver avec demi-cylindre infini - on écrase le cylindre pour que son rayon soit exp(-y) : il est de plus en plus fin en approchant de l'infini (quand on monte)
- on le regarde d'au dessus : on voit le disque épointé
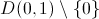 (un peu comme si on l'aplatissait sur le plan)
(un peu comme si on l'aplatissait sur le plan)- le point 0 est alors le point à l'infini de la bande de départ
Je sais pas si c'était très clair, voici un petit dessin si ça peut aider :
4) Le groupe modulaire
Le demi plan de Poincarré est l'ensemble
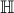 défini par
défini par 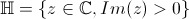 . C'est le demi plan
supérieur.
. C'est le demi plan
supérieur.Sur
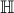 il existe une action du groupe
il existe une action du groupe 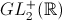 (l'ensemble des
matrices 2x2 de déterminant positif) qui agit par g :
(l'ensemble des
matrices 2x2 de déterminant positif) qui agit par g : 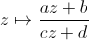 . Cette action se
restreint à celle de
. Cette action se
restreint à celle de 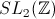 car c'est un sous groupe. L'action de -Id est triviale car
car c'est un sous groupe. L'action de -Id est triviale car 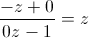 , donc finalement
c'est
, donc finalement
c'est  qui
agit sur
qui
agit sur 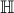 , de
façon fidèle, et hautement non transitive. On
note ce groupe
, de
façon fidèle, et hautement non transitive. On
note ce groupe 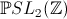 ,
et on l'appelle le groupe modulaire !
,
et on l'appelle le groupe modulaire !On peut d'abord prouver plusieurs choses :
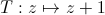 et
et 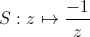 sont dans le groupe
modulaire. De plus ce sont des générateurs de
sont dans le groupe
modulaire. De plus ce sont des générateurs de 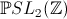 .
Enfin on peut montrer que ST est d'ordre 3, S est d'ordre 2,
et
décrire ainsi mieux la façon dont S et ST engendrent le groupe (voir l'illustration sur la figure suivante).
.
Enfin on peut montrer que ST est d'ordre 3, S est d'ordre 2,
et
décrire ainsi mieux la façon dont S et ST engendrent le groupe (voir l'illustration sur la figure suivante).La recherche de domaines fondamentaux revient à chercher un ensemble contenant exactement un représentant de chaque orbite. Il en existe un pas trop compliqué :
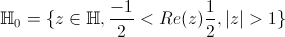
On peut illustrer
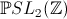 en le voyant comme un ensemble de domaines fondamentaux : sur [ -1.6 , 1.6 ] + i [ 0 , 3.2 ]
en le voyant comme un ensemble de domaines fondamentaux : sur [ -1.6 , 1.6 ] + i [ 0 , 3.2 ]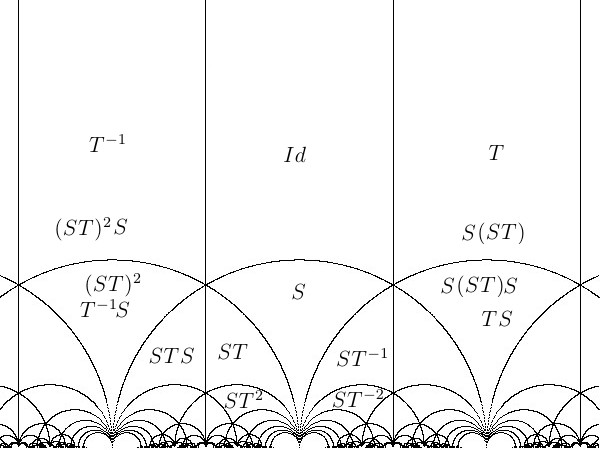
 est le domaine noté Id : en fait le domaine u désigne u(
est le domaine noté Id : en fait le domaine u désigne u( ). On voit que
). On voit que  est envoyé sur le domaine en dessous de lui par la symétrie S. La
translation T décale le domaine sur la droite, et ST lui fait faire une
rotation autou du point j=exp(2i
est envoyé sur le domaine en dessous de lui par la symétrie S. La
translation T décale le domaine sur la droite, et ST lui fait faire une
rotation autou du point j=exp(2i /3).
/3).Pour Bob, si ça va un peut vite, en plein milieu, tout en bas c'est le point 0. À sa verticale, entre les domaines notés Id et S, il y a i.
Un plan plus large des domaines fondamentaux est disponible à la page Homographies !
f est modulaire de poids k signifie
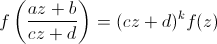 , pour toute
application de
, pour toute
application de 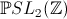 ,
et pour tout complexe de
,
et pour tout complexe de  . Il faut aussi que la fonction soit holomorphe à l'infini.
. Il faut aussi que la fonction soit holomorphe à l'infini. Cette deuxième condition signifie f est holomorphe en 0 après le changement de variables
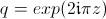
On remarque tout de suite que f(z+1)=f(z) donc les fonctions modulaires sont 1-périodiques.