Lecture sur les graphes

1) Les valeurs

Il faut bien avoir en tête les valeurs qui correspondent aux complexes. Pour cela avoir le graphe de l'identité ouvert à côté peut être utile. 

  Graphe de la fonction identité sur [-2,2] + i [-2,2]                       Même fonction identité sur [-100,100] + i [-100,100]
   
      Au milieu, on voit 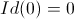 car un point noir apparaît. Le graphe de gauche est globalement sombre car les valeurs du module de la fonction sont petites sur le rectangle qu'on a évalué. On voit que la courbe de couleur Cyan (resp. Rouge) décrit les points dont l'image est réelle positive (resp. négative). Ici ce sont précisément les points réels (car Id stabilise 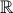) pour les deux graphes.
    Le deuxième graphe est une dilatation du premier : on a ramené les valeurs du graphe de gauche vers 0. On regarde donc la fonction de plus loin.  Le graphe est globalement plus clair car la fonction prend des valeurs plus grandes (en module). Le zéro reste visible. On voit aussi que la rotation des teintes est proportionnelle à l'argument des points : les courbes de même couleur sont des droites passant par zéro (c'est spécifique à cette fonction bien sûr).

La fonction conjugué 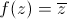sur [-2,2] + i [-2,2]                  La fonction inverse : 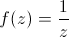        sur [-2,2] + i [-2,2] 
   

   La conjugaison (gauche) fait les mêmes luminosités que l'identité. Les teintes sont parcourues à l'envers : le graphe est le symétrique par rapport à l'axe horizontal, de celui de l'identité. On peut donc distinguer ainsi une symétrie.
   Pour la fonction inverse (droite) le module en zéro tend vers l'infini, donc le point central est affiché en blanc. En regardant ces deux images, on remarque aussi que la variation des teintes est la même pour les deux fonctions. Cela traduit la propriété :

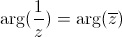
2) Zéros et pôles, simples ou multiples

   À partir d'ici, les intervalles de traçage des fonctions seront toujours [-2,2] + i [-2,2] :            

Graphe d'une fonction linéaire : 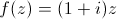                          Graphe d'une fonction affine    :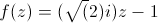
                                         
  Les deux sont tracées sur [-2,2] + i [-2,2]. Finalement, les graphes des fonctions affines (et injectives) sont des déplacements (rotations, translations) et homothéties du graphe de l'identité. Rien de très surprenant (c'est le cas aussi des représentations sur ).

Un polynôme :  
         

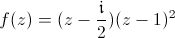
    Le fait que le zéro est double en 1 se remarque car l'argument fait deux tours. Le nombre de tours de l'argument autour d'un zéro ou pôle est toujours sa multiplicité : cela traduit le fait que l'équation 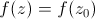a autant de solutions que la multiplicité du zéro (sur un voisinage).


Une fraction rationnelle :
               

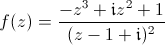
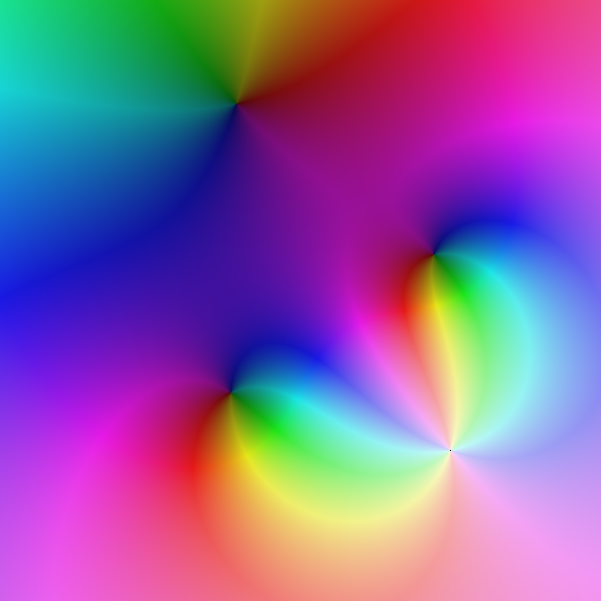
    Le pôle est double donc l'argument fait deux tours au point brilliant ; les zéros sont simples, l'argument ne fait qu'un tour


3) Continuité

     La continuité des fonctions se voit au fait que les couleurs varient continûment : aucun changement brutal de teinte ou de luminosité (on n'a tracé que des fonctions continues jusqu'ici). Par ailleurs les discontinuités ponctuelles ne se distinguent pas si la fonction admet un prolongement continu au point.
     Lorsque l'on a un pôle, il apparaît en BLANC et ne donne pas de discontinuité de couleur (alors que la fonction est discontinue). Mais vue comme une fonction vers 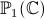, un pôle n'est pas un point de discontinuité. Donc, c'est pas trop grave.
     Lorsqu'on a une singularité essentielle (voir page Singularités) la discontinuité est assez visible...
     
     Voilà pour les discontinuités ponctuelles. Un exemple de discontinuité non-ponctuelle avec le logarithme :

Fonction logarithme :
                   

     Le logarithme n'a pas de prolongement continu sur 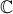privé de 0. On est obligés de choisir une droite (ou n'importe quelle courbe injective reliant 0 à l'infini) sur laquelle le logarithme est discontinu, à cause de la discontinuité de l'argument. Ainsi le choix d'un argument détermine un logarithme. La discontinuité est bien visible sur le dessin.
   On peut faire beaucoup de déterminations différentes de cette fonction, quelques unes sont présentées à la page Déterminations !
    Le problème du prolongement d'un germe de logarithme est illustré à la page Séries entières !


4) Dérivées

Pour voir un point d'annulation de la dérivée, deux cas de figures :
  - La fonction s'annule aussi, alors il y a un zéro double : on voit deux tours de l'argument autour du point noir
  - La fonction ne s'annule pas mais l'équation locale 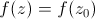a au moins deux solutions. Cela se voit donc en trouvant au moins deux courbes de même teinte qui se croisent.

Le cosinus : 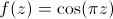                                                        Le monôme :
     
À gauche : il n'y a pas de zéros doubles de la fonction. En revanche les courbes rouge et bleu clair vérifient la deuxième propriété. Elles se rencontrent aux points de , soit les zéros de sa dérivée  .
À droite : un zéro double (car il est triple) de la fonction en 0. Il est plus visible que les points critiques de 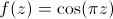, car il vérifie la deuxième propriété pour toutes les teintes alors que pour le cosinus, il n'y en a qu'une qui marche en chaque point critique.

   Les propriétés de dérivées d'une fonction sont possible à visualiser "en gros" sur les graphes, mais ne sont pas aussi lisibles que celles qu'on a vues jusqu'ici. En voyant un graphe en pratique, on ne pourra même pas conjecturer qu'elle est holomorphe

   On va maintenant voir comment lire la dérivabilité :
La dérivabilité au sens complexe signifie l'existence du nombre dérivé. En terme de calcul différentiel sur , cela signifie encore que la différentielle est nulle ou que c'est une similitude directe (une transformation  qui conserve les angles).  Tout cela est bien sûr local.

Pour qu'une fonction soit dérivable (holomorphe) : les courbes d'équimodule et les lignes de même argument doivent former un angle de +90° (l'orientation est difficile à formaliser mais en pratique elle se voit un peu).

L'identité et l'exponentielle :
           

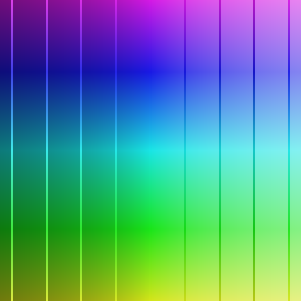
  Pour l'identité, les droites passant par zéro (lignes de même argument) sont bien orthogonales localement aux cercles centrés en zéro (courbes d'équimodule).
   Pour l'exponentielle, c'est encore plus clair car toutes ces courbes sont des droites, elles sont toutes orthogonales les unes aux autres.

La conjugaison et :  
              

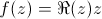    Pour la conjugaison complexe (à gauche), ce qui met en défaut la dérivabilité est le sens de rotation de l'argument autour de 0. Donc l'image de l'angle formé par l'intersection de deux courbes est -90° au lieu de +90°... (vraiment avec les mains !)
    Pour celle de droite, elle n'est pas holomorphe (on peut vérifier avec les équations de Cauchy-Riemann) et ça se voit en regardant attentivement les angles formés par les deux types de courbes : ils ne sont pas droits (ou rarement).

    Normalement, Bob est plutôt armé pour saisir un peu le sens des représentations complexes. Si il n'a pas compris la signification des couleurs, peut-être devrait-il regarder la page Mode de représentation !
    Sinon, pour voir les fonctions classiques RDV sur Fonctions principales !
     Pour voir des fonctions un peu plus exotiques, RDV sur la page Singularités ou Fonction zeta ou Fonctions modulaires !