Tutoriel :
comment utiliser le programme Mandelbrot
Ce tutoriel présente l'utilisation du programme Mandelbrot ici ! L'ensemble de Mandelbrot est un ensemble fractal défini par une "équation". Il s'agit d'un ensemble décrivant le comportement d'un système dynamique (divergence ou convergence), le détail est sur la page Ensemble de Mandelbrot !
La réalisation de ces programmes a été un travail considérable. Je l'ai rendu public et ainsi je ne peux poser aucune restriction concernant l'utilisation des programmes et images du site (et je ne le souhaite pas d'ailleurs, bien au contraire).
En revanche je demande explicitement à tout visiteur du site de ne pas en plagier le contenu pour faire penser que ce travail est le sien. Si vous utilisez ceci à des fins scientifiques, citez moi, merci d'avance.
1) Commandes de base (souris)
Pour commencer, le mieux est de cliquer sur un des boutons "dessiner le Mandelbrot", vous vous retrouverez avec ceci :
Il s'agit donc de l'ensemble de Mandelbrot, un exemple assez célèbre de fractale. Comme le suggère la page, on peut cliquer sur l'image pour zoomer. Lorsqu'on clique, le point saisi devient le centre de l'image, et le zoom est en x2.
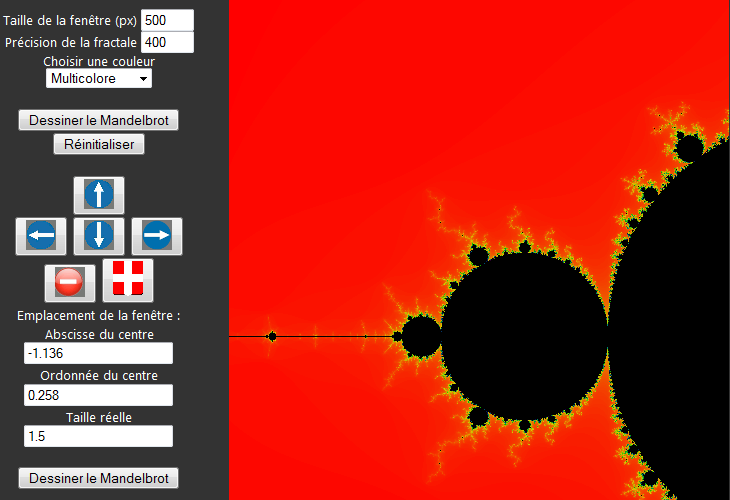
Comme on peut le voir, les paramètres sur la gauche évoluent de façon interactive, ce qui peut permettre de mémoriser l'emplacement exact d'une image affichée. On y reviendra juste après. On peut aussi se déplacer manuellement avec les flèches de direction
et les boutons zoom/dézoom (sens interdit 
/savoie ! 
), qui font eux aussi un facteur x2 et :2 sur la taille de l'image.2) Les paramètres
Le premier paramètre est la taille (en pixels) voulue pour l'image. J'ai mis une taille maximale de 1200px, c'est amplement suffisant me semble-t-il. Si vous souhaitez une plus grande image le mieux est de me contacter pour que je la produise. Mon adresse est
. J'ai fait en
sorte que le programme ne puisse pas planter, il fallait pour cela
empêcher l'utilisateur de surestimer son processeur.
Par exemple, si votre ordi est très lent, ou que vous souhaitez générer les images vite (par exemple pour trouver en endroit particulier), vous pouvez réduire la taille d'image.
Un deuxième facteur intervient sur le temps de calcul du programme : je l'ai appelé "précision de la fractale", ou "itermax". Pour comprendre le sens exact de ce terme vous pouvez voir la page Ensemble de Mandelbrot !
Mais sinon en pratique voilà comment il intervient :
Itermax : 400 Itermax : 1000
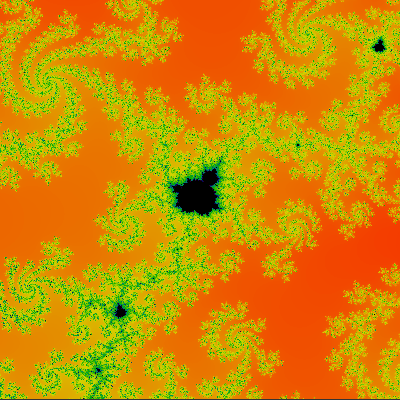
Augmenter le nombre de la précision de fractale augmente justement l'aspect fractal du dessin. Là sur un ilôt de Mandelbrot on voit bien que la deuxième est plus juste mathématiquement. Par contre (et on le voit aussi ici) cela crée un réétalonnage des couleurs et c'est pour ça que j'ai pas programmé son augmentation par défaut lorsqu'on zoome.
Un dernier mot : ces "problèmes" n'apparaissent que lorsqu'on a déjà bien zoomé. Ici la taille réelle de l'image est 0.0029296875 ce qui est tout de même assez petit. J'ai plafonné itermax à 2000, car au delà votre navigateur ne va pas aimer de toute façon (et en plus ça ferait planter le programme et je le voulais implantable).
Les 3 autres paramètres décrivent la position géométrique de la fenêtre :
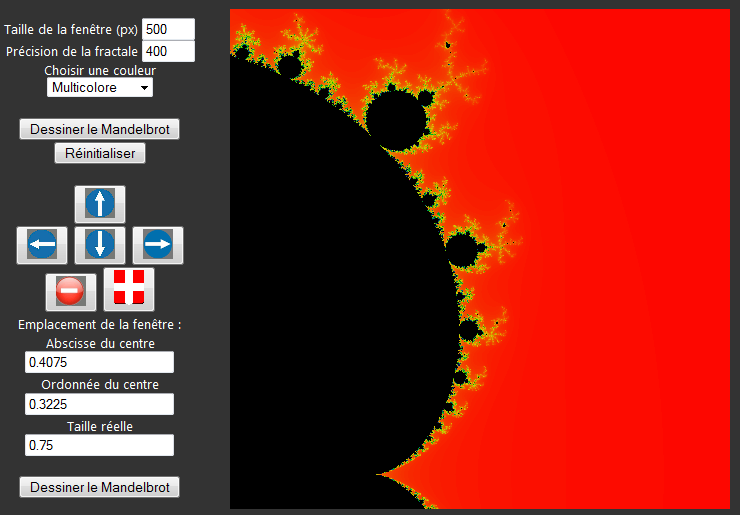
L'ensemble de Mandelbrot est un sous ensemble de
,
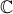on peut savoir ainsi où il est. Par exemple au tout départ, le carré de
réprésentation est [ -2.3 , 0.7 ] + i [ -1.5 , 1.5 ]. Ici, le carré
représenté est le carré de centre ( 0.4075 , 0.3225 ) de côté 0.75 .À tout moment on peut les mettre à jour manuellement si l'on pense connaître une position du Mandelbrot intéressante à regarder.
3) Couleurs
J'ai proposé 5 modes de couleur qui présentent tous des intérêts esthétiques ou mathématiques différents. Je peux vous en dire les très grandes lignes mais après seule l'exploration personnelle vous permettra d'en juger. Le plus polyvalent est le "Multicolore" :
De près, de loin, avec un itermax balaise ou pas, il en jette et il est assez précis.
Après les deux sans couleurs sont plus viables "mathématiquement".
À gauche c'est noir & blanc, à droite nuances de gris. Noir & blanc a pas beaucoup d'intérêt ici, mais un peu plus sur les ensembles de Julia : parfois il permet de mieux réaliser par exemple, que l'ensemble est presque vide alors que les autres modes d'affichage ne le montrent pas. Le "Nuances de gris" a vraiment la classe de près, mais de loin moins.
Pour les deux suivants c'est le contraire :
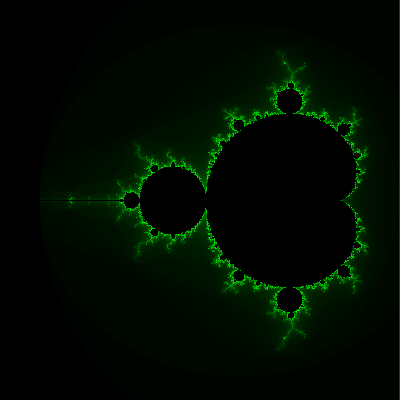Les deux en jettent pas mal de loin mais sont moins précis de
près. C'est un vrai casse tête de définir des couleurs.