Ensembles de Julia
Les ensembles de Julia sont définis par une équation assez similaire à celle de l'ensemble de Mandelbrot :
1) Définition & première propriété
Soit C une constante complexe. L'ensemble de julia
 associé à C est défini de la façon suivante :
associé à C est défini de la façon suivante : Un nombre complexe
 lorsque la suite définie par :
lorsque la suite définie par :  est une suite bornée.
est une suite bornée.
Pour une définition ressemblante de l'ensemble de Mandelbrot, on dirait :
Un nombre complexe C est dans est dans le Mandelbrot lorsque la suite :
 (ou
(ou  ) est une suite bornée.
) est une suite bornée.
On voit une certaine similitude, ce n'est pas un hasard : l'ensemble de Mandelbrot décrit précisément les ensembles de Julia connexes. (Connexe signifie "en un seul morceau"). Un exemple :



Ici on voit que le Julia défini par une constante hors du Mandelbrot est en plusieurs morceaux. En fait si on change le mode de réprésentation : en mettant NOIR & BLANC, on voit qu'en vrai le Julia de droite est beaucoup plus vide :


Et là j'ai triché pour qu'on voie quelque chose, en réalité, en laissant un itermax de 400 (moi j'ai mis 50) le dessin de droite serait juste complètement noir. En fait les ensembles de Julia dont la constante est en dehors du Mandelbrot sont presque vides : ils sont d'aire nulle, leurs composantes connexes sont des singletons (ce qui signifie qu'il n'y a jamais "2 points qui se touchent"). Cela n'empêche pas de faire de jolies images, mais les ensembles mathématiques sont beaucoup plus pauvres.
Moralité : l'ensemble de Mandelbrot résume les ensembles de Julia.
2) De Mandelbrot à Julia
On peut en fait remarquer que même les principales composantes de l'ensemble de Mandelbrot déterminent une forme globale aux ensembles de Julia. Voici un bref résumé des types de Julia qu'on trouve en fonction de la constante choisie.
A) Les julias dans la Cardioïde
Voici la forme de quelques Julias dont la constante est choisie dans la CARDIOÏDE :

On ne manquera pas de constater une certaine ressemblance, toutes ces figures sont homéomorphes au cercle. On reconnaît le cercle pour la constante (0,0) et les autres en sont des déformations bicontinues.
B) Les Julias dans D(-1,1/4)
Voilà les Julias qu'on rencontre dans le plus gros cercle de l'ensemble de Mandelbrot :

À nouveau ils se ressemblent pour la même raison : ils sont homéomorphes. (si vous ne comprenez pas le sens, vous comprendrez certainement l'interprétation géométrique)
C) Le lapin de Douady :
Un Julia assez célèbre est le lapin de Douady, Adrien Douady l'a présenté sur des vidéos de vulgarisation des ensembles de Julia, et notamment avec un film : la dynamique du Lapin. Il ressemble à ça :

Et on voit qu'on peut le trouver sur le cercle du haut. En l'observant on constate que le corps est toujours relié à 2 oreilles (d'où son nom de Lapin). En prenant la constante dans un autre endroit du mandelbrot, on peut avoir quelque chose d'assez similaire, où le corps est relié à 3 oreilles, ou 4 ou 5..
D) Le lapin à 3 oreilles
Voici par exemple des Julias qu'on trouve dans un autre disque, qui on plus d'oreilles que le lapin de Douady :

E) En résumé
Voici une image qui résume un peu tout ça, mais le mieux est de le voir de vos propres yeux sur Application Julia !

Et là on voit plein de types de Julia différents en fonction de la position géométrique de leur constante C. J'en ai mis 3 très reconnaissables, dont la constante est à l'extérieur du Mandelbrot.
3) Et quand on traverse la frontière...
Mathématiquement, la question peut se poser (je n'en ai pas la réponse) : est-ce que l'application qui à un C fait correspondre son ensemble de Julia
 est continue
? Il faut pour cela munir les compacts du plan de la distance de
Haussdorf par exemple (pour définir la proximité topologique de 2
ensembles du plan).
est continue
? Il faut pour cela munir les compacts du plan de la distance de
Haussdorf par exemple (pour définir la proximité topologique de 2
ensembles du plan). On a déjà vu que la déformation des Julias semble continue lorsqu'on reste dans le même morceau du Mandelbrot. En fait en changeant de morceau du Mandelbrot la déformation est assez continue aussi :

J'ai mis une approximation de la constante de fin pour donner l'emplacement approximatif. L'idée est de passer de la cardioïde à un cercle et d'observer la déformation progressive des Julias. On remarque qu'elle est "assez continue" quand on a assez zoomé, et comme le niveau de zoom nécessaire dépend beaucoup du point où l'on se trouve il est certain que ce n'est pas une continuité uniforme sur
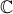 . Je ne sais pas si il a des théorèmes validant cette observation.
. Je ne sais pas si il a des théorèmes validant cette observation.Par ailleurs lorsqu'on sort du Mandelbrot les Julias se fragmentent de façon à priori plus violente :

Comme les points dans l'ensemble de Julia sont affichés en noir, il semble impossible que cette transformation soit continue à la traversée de la frontière : le julia a littéralement explosé lors de la traversée.
4) Julias d'un mini-mandelbrot
Une dernière observation que j'ai pu faire : les ensembles de Julia d'un mini-mandelbrot sont des mini-julias reprenant les mêmes formes mais de façon beaucoup plus localisée :
On commence par trouver un mini mandelbrot et dessiner le Julia :

Maintenant on zoome sur tous, pour le Julia on vise les plus gros points. Puis on choisit une constante un peu à côté (je l'ai entourée en blanc) pour refaire un Julia qu'on connaît sur le gros Mandelbrot :

Et ça refait un mini-lapin ! (et même des tas d'autres encore plus petits)
J'espère que la visite guidée vous a plu, vous pourrez observer beaucoup d'autres choses en allant voir Application Julia !