L'ensemble
de Mandelbrot
Sur cette page, vous pourrez voir la définition mathématique de l'ensemble, quelques informations sur l'histoire de son étude et quelques petites choses que vous pourriez éventuellement observer sur la page Application Mandelbrot !
1) Définition
L'ensemble de Mandelbrot caractérise le comportement du système dynamique suivant dans
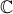 :
: 
La question est la suivante : pour quelles valeurs de c cette suite reste-t-elle bornée ? La réponse :

L'ensemble des points affichés en NOIR sur ce dessin décrit précisément les points d'orbite bornée sous l'action de ce système dynamique. L'ensemble est FRACTAL. C'est dur à définir formellement mais facile à voir : des motifs se répètent à l'infini lorsqu'on zoome sur n'importe quel point de la frontière.
Voici une des premières illustrations informatiques qu'en a fait Benoît Mandelbrot avec un "ordinateur" IBM :

Bien sûr la puissance de calcul n'était pas comparable à celle du plus mauvais ordinateur en commerce aujourd'hui : la plupart des calculatrices de collège surpassent largement la puissance de calcul dont il disposait alors...
En fait, pour savoir si un nombre complexe est dans l'ensemble, on peut définir un itermax (que j'ai noté "précision de la fractale") qui va être considéré comme l'infini. On choisit un pixel (x,y), en fonction de la position de la fenêtre on trouve le nombre complexe c=a+ib correspondant. Ensuite on regarde les valeurs prises par la suite :
(..(c²+c)²+c)..)²+c on répète cette opération tant que la norme du résultat est inférieure 2. Si à l'étape itermax la suite ne s'est pas encore échappée à l'infini, alors le point est considéré comme étant dans l'ensemble de Mandelbrot. Idéalement il faudrait un itermax le plus grand possible mais pour l'éxécution du programme sur internet, j'ai fixé sa valeur maximale à 2000.
Le seul tracé mathématiquement viable est celui en Noir & Blanc, pour les autres on parcourt les couleurs en fonction du temps que ça a mis à diverger. Ainsi on peut deviner l'existence des branches les plus fines s'échappant du Mandelbrot sans en voir aucun des points.
2) Histoire
L'ensemble porte le nom de Benoît Mandelbrot mais il a été d'abord étudié (créé) par Gaston Julia et Pierre Fatou, et il est rigolo de noter que tous ces gens sont Français ! (Mandelbrot est né en Pologne). C'est aussi un Français qui a sorti la plupart des théorèmes liés à cet ensemble, il s'agit de Adrien Douady, décédé en 2006. C'est lui qui lui a donné ce nom.
Les mathématiques n'appartiennent pas encore aux américains, l'actuel médaille Fields (2010-2014) est lui aussi Français, il s'appelle Cédric Villani et il a prouvé un théorème de minoration de l'entropie créée (et probablement des tas d'autres choses).



Je ne pense pas qu'on m'en voudrait de diffuser leurs photos. De Gauche à droite : Benoît Mandelbrot, Adrien Douady, Gaston Julia. Gaston Julia a été blessé à la première guerre mondiale et a porté un masque de cuir le reste de sa vie.
Un des théorèmes que Douady a établi est : "L'ensemble de Mandelbrot est connexe" (en un seul morceau) et même un peu plus que ça : le complémentaire dans
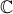 de l'ensemble de Mandelbrot est conformément
équivalent au complémentaire du disque unité.
de l'ensemble de Mandelbrot est conformément
équivalent au complémentaire du disque unité.3) Quelques propriétés
On a déjà dit que l'ensemble est en un seul morceau, et même qu'il n'a pas de "trous" (c'est la deuxième partie de l'énoncé ci-dessus).
Il est facile de voir qu'il est inclus dans
 . Pour les grandes
lignes, il est constitué d'une cardioïde et de pas mal de cercles (une
infinité :)
. Pour les grandes
lignes, il est constitué d'une cardioïde et de pas mal de cercles (une
infinité :) La cardioïde Le plus gros cercle : centre (-1,0), rayon 1/4


Le point (-2,0) est sur la frontière du Mandelbrot. C'est le point de plus grand module qui soit dans l'ensemble. De plus, le sommet de la cardioïde est le point (1/4, 0) :
Sommet de la cardioïde

4) Petite visite guidée
Voici quelques observations qu'on peut faire sur l'ensemble de Mandelbrot :
Les ilôts de Mandelbrot sont des mini-ensembles de mandelbrot qu'on voit surgir un peu n'importe où quand on zoome. Pour les observer bien je vous conseille d'augmenter la valeur par défaut de "précision de la fractale", surtout si vous en visez un petit.

Là on voit 2 ilôts de Mandelbrot, ceux là sont assez gros.
La vallée des hippocampes : les strilles s'échappant du Mandelbrot rappellent des queues d'hippocampes :

Un peu partout sur la frontière on peut aussi observer des tourbillons (je ne sais pas si ils ont un nom officiel).

Et voilà pour la visite guidée. L'article wikipédia est très riche sur le sujet, je vous suggère de le lire si le domaine vous intéresse.
5) Autres fractales
Il existe d'autres fractales qu'on peut créer en lien avec l'ensemble de Mandelbrot. En voici deux exemples que Jean-Florent Raymond a tracées informatiquement :
Le buddhabrot :

C'est un ensemble probabiliste qui présente grossièrement les orbites de l'itération f(x)=x²+c (la fonction décrivant le mandelbrot) pour les points qui s'échappent à l'infini. On peut alors voir les zones plus attractrices dans le mandelbrot. Et en plus il ressemble à Buddha ! Il faut pas mal de puissance informatique pour construire cette image, du coup on n'en a pas fait beaucoup.
L'anti-buddhabrot :

Il a une définition assez similaire, il décrit les orbites des points qui ne s'échappent pas à l'infini. Les deux évoquent la forme du Mandelbrot à ceci près qu'on les a fait pivoter (artificiellement) pour l'aspect esthétique.