Il y a plusieurs contextes dans lesquels les homographies ont des propriétés intéressantes. Elles permettent par exemple de réaliser les bijections holomorphes de deux types d'ouverts. Dans un contexte un peu différent elles réalisent les bijections de 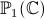 et permettent de faire des changements de cartes projectifs. Une certaine classe d'homographie permet aussi de définir les fonctions modulaires.

1) Bijections holomorphes du disque

    Dans cette section on tracera les graphes sur les pavés [-1.1 , 1.1] + i [-1.1 , 1.1]. Par ailleurs on change le mode de représentation de sorte que les points dont le module de l'image dépasse 1 s'affichent en noir (tout en gardant la couleur continue).

     La théorie donne toutes les bijections du disque unité sur lui même : 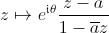  où les deux paramètres  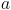et 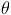sont choisis respectivement dans le disque, et dans 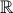. Pour 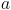= 0  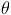,  =0 , la fonction est l'identité.

En voilà une avec 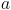= -0.6 + 0.21 i   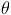,  =1
                     
                        
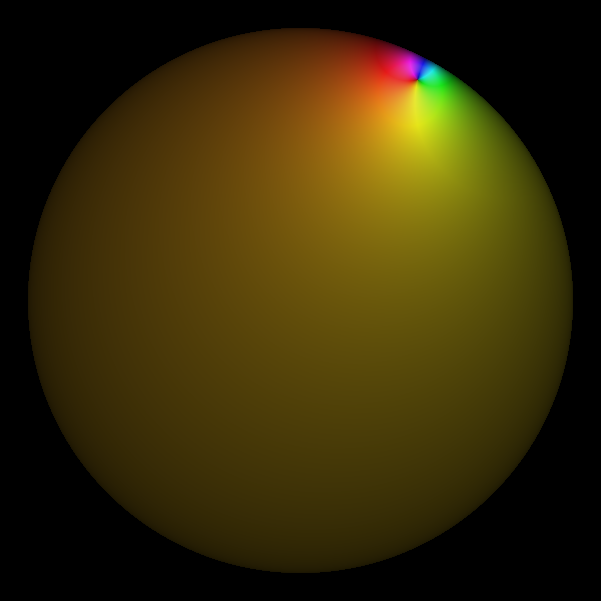
   Le point 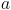est reconnaissable car il annule la fonction. Cette homographie a un pôle situé en dehors du disque. La fonction a un point fixe situé sur la frontière (mais il n'est pas reconnaissable).

   En voici une autre avec 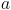= 0.43 + 0.81 i  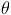 ,  =4.02 :
                     

        Il est naturel de prendre des homographies pour une telle ambition, car elles envoient les cercles-droites sur des cercles-droites. Ainsi c'est aussi une homographie qui permet de réaliser une bijection de sur . Alors on peut en déduire les bijections du demi-plan de Poincarré.

2) Bijections holomorphes du demi-plan

      On définit le demi-plan de Poincarré  . On peut trouver toutes ses bijections holomorphes.
Pour cela on transporte le cercle unité sur la droite réelle par l'application .
                     

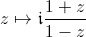     Le disque est envoyé de façon bijective et holomorphe vers le demi-plan de Poincarré : ça se voit sur les couleurs prises par la fonction en plein centre. Ensuite, on retrouve les bijections de 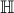: il s'agit des homographies réelles : où a,b,c,d sont réels et  ad-bc >0.

Exemple : avec a=1 , b=-2 , c=2 , d=1 sur le carré [-3,3] + i [-0.1 , 5.9 ] :
                         

      On a toujours un zéro et un pôle réels, les valeurs prises sur sont exclusivement dans .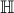

Cette partie est adressée à un public familier des actions de groupes et des nombres complexes.
Vous pouvez passer directement à la partie 3  si ces sujets ne vous passionnent pas :)

En fait des groupes de matrices agissent sur 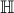par l'application décrite ci-dessus : c'est l'action de 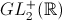. Cette action se restreint à celle de 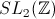. Pour que l'action soit fidèle on quotiente par le sous-groupe à deux éléments, on fait donc agi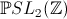r sur 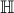. En observant les orbites, on peut classifier les réseaux de 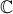: les classes d'homothécies de réseaux sont décrites par un unique (ou presque) élément d'un domaine fondamental.
   Ensuite on peut faire agir le groupe 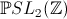sur les domaines fondamentaux du plan, ce qui découpe une partition de :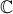

                         

Quelques domaines fondamentaux sur [ -1.6 , 1.6 ] + i [ 0 , 3.2 ].
        Il faut remarquer plusieurs choses : le shéma se répète par translation de 1 vers la droite ou la gauche. Pour en voir l'illustration sur les réseaux, voir le GIF weierstrass situé sur la page Singularités. Cela tient juste au fait que l'application  T: est dans . Par ailleurs l'application S: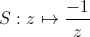 est aussi dans le groupe modulaire. Ces deux éléments suffisent à générer le groupe. Pour plus de détails sur le groupe modulaire et les domaines fondamentaux, voir la page Fonctions modulaires !



3) Transport de domaines

   Avec des Homographies on peut donc transporter des domaines de définition de fonctions de façon à rendre visibles des points éventuellement loins ou infinis. Par exemple, l'application 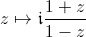 décrite précédemment permet de dessiner dans le disque unité une fonction définie sur . Par exemple une sorte de série de Dirichlet : on additionne les . Cette famille de fonctions est sommable sur le demi-plan de Poincarré. On peut la représenter dans le disque unité pour faire apparaître le comportement de la limite sur les branches infinies de .

   Et la limite tracée sur le disque donne donc ceci :
                     

          On peut imaginer ce qu'il reste de la période réelle de la fonction qu'on a dessiné à cause de la répétition du motif en s'approchant de -1. La représentation n'est bien sûr pas isométrique.

Cette partie est adressée à un public familier des changements de variables et des nombres complexes.
Vous pouvez passer directement à la partie 4  si ces sujets ne vous passionnent pas :)

    Il y a une autre façon de dessiner des fonctions de 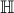dans le disque, il s'agit de faire la même opération avec le changement de variable 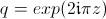, et en regardant la fonction comme si elle était définie sur D(0,1). Cela requiert tout de même de s'assurer que la fonction a une période 1, ce qui est toujours le cas pour des fonctions modulaires. C'était aussi le cas de la fonction qu'on a tracée ici, avec un petit changement de variable on pouvait lui attribuer une période 1. Ce changement de variable sera alors plus commode.
Donc en regardant la fonction 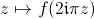   et en opérant le changement de variable décrit au dessus, on trace alors 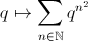  sur le disque unité :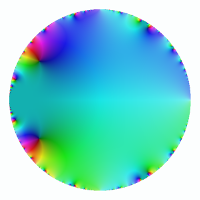
                                                                 
     Nous avons tracé exactement la même fonction, mais le changement de variable était différent.  Cela revient à identifier le disque avec 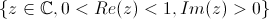, donc plus qu'une bande verticale du demi-plan de Poincarré, d'épaisseur 1. Le point infini est envoyé au milieu du disque, car 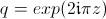 ne s'annule que quand z tend vers l'infini. Forcément cette représentation est plus précise (car elle décrit un domaine plus petit) mais on ne peut la tracer que lorsque les fonctions ont une période 1. Dans le cas contraire, on perd les informations contenues dans les autres bandes verticales que celle où on a tracé la fonction.  Pour plus de détails sur ce changement de variables, voir la page Fonctions modulaires, où on le fait à chaque fois !

En tout cas, ce changement de variables n'avait rien d'une homographie...

4) Bijections de l'espace projectif

   On n'a pas dit jusqu'ici que les homographies réalisent exactement les bijections de l'espace projectif 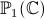. Pour la suite, on considèrera 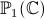comme 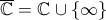, avec la topologie projective (celle du compactifié d'Alexandrov), je n'entrerai pas plus dans les détails de l'aspect topologique. Mais on peut les définir sur 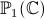 grâce au fait qu'on peut y définir une limite (infinie) sur le pôle d'une homographie au sens de l'espace projectif. De plus les homographies ont une limite à l'infini (sauf les homographies affines, alors elles valent l'infini à l'infini).

Soient 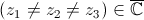, alors il existe une unique homographie 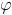 telle que   . De plus elle est donnée par la formule

    L'exemple le plus simple : : il échange de place les points 0 et infini, et laisse 1 à sa place, et le cercle unité est juste "retourné". Le mieux est de l'illustrer : avec  une fraction rationnelle :
   

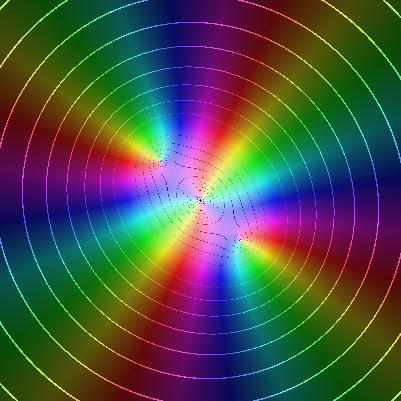
   À gauche c'est la fraction rationnelle 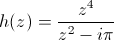représentée de façon standard sur [-2,2] + i [-2,2]
   À droite c'est la même fonction h composée avec f : 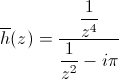   .  Et en fait, on peut l'interpréter comme un changement de carte de représentation de la fonction h. C'est comme si on avait dessiné la fonction h en retournant la sphère de Riemann, échangeant les places de zéro et l'infini. Alors, ce qu'on voit à droite est le comportement de h à l'infini, soit un pôle double. Cela était prévisible en y réfléchissant : 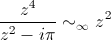 , donc la singularité est un pôle d'ordre 2.
Pour revoir ce changement de variable, RDV sur Fonction zeta !

Un autre exemple :

   Au lieu d'échanger 0 et l'infini, on peut choisir la place de 3 points distincts quelconques. Il peut être intéressant de voir à la fois 0, l'infini et 1 sur une même carte :
On le fait avec l'application 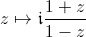(qu'on a déjà vue plus haut !) pour la fonction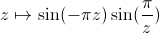
             

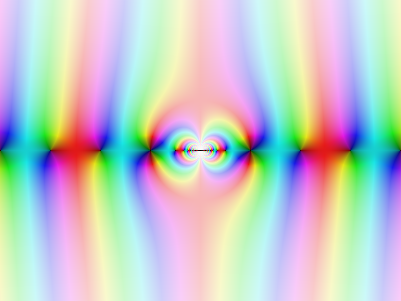
   À gauche la fonction est représentée sur [-4,4] + i [-3,3]. Une singularité essentielle comme on pouvait s'y attendre.
   À droite , on a plié l'infini, 0 et 1 sur le cercle unité : la fonction est représentée sur [-2,2] + i [-2, 2]. L'aspect symétrique vient du rôle symétrique par rapport à 1 de z et 1/z  géométriquement et dans la définition de la fonction tracée.

Le changement de carte projectif revenait à prendre dans le choix du changement de carte projective.
Alors, on voit ici qu'on a replié 0 et l'infini à un rôle symétrique, et que les deux singularités apparaîssent sur notre carte.

Pour revoir ce changement de variables, voir la page Déterminations !


   Un dernier exemple : rapprocher l'infini

Voilà une déformation du logarithme en rapprochant et déplaçant l'infini : sur le carré [-5,5] + i [-5,5].
z1=0 ; z2=1 (ils sont inchangés par l'homographie) et z3 (le point envoyé à l'infini) varie dans le plan :

                         z3= -10 + 10 i                                                                                 z3=-1 + i
                                 
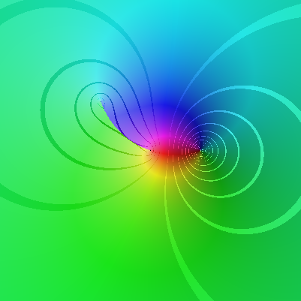
                                     z3= -1- 2i                                                                               z3= 1.4 - 0.4 i
                           

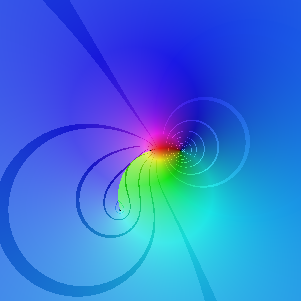
    Au plus on rapproche l'infini d'un des deux points fixés, au plus la fonction est "constante"(en fait c'est pas exactement ça...). La déformation des lignes d'équimodules permet de bien situer le déplacement des points du plan lors du changement de variable.

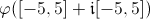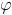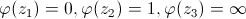       Pour bien comprendre le sens de ces représentations, il faut bien voir que les 4 fois, on a représenté la même fonction. Il est bon de voir aussi que cela revient à représenter la fonction sur où est l'homographie vérifiant . En gros, ça permet de tracer la fonction sur un "rectangle infini", qui n'a plus grand chose d'un rectangle car les segments des bords peuvent être envoyés sur des arcs de cercles.

     Pour l'exemple du logarithme, on peut aussi remarquer que la discontinuité se contente de relier les deux points 0 et l'infini par une courbe. Sur la dernière image, on a z1=0, z2=1, z3 est pas loin d'eux, on voit que les rôles des discontinuités en 0 et en l'infini sont très similaires.
On imagine alors des déterminations du logarithme qu'on peut déduire en prolongeant la détermination principale sur D(1,1). On y revient plus en détails dans Déterminations, où l'on va trouver plusieurs façons de déterminer le logarithme, en choisissant d'autres façons de répartir ses discontinuités...

Pour plus de singularités replacées dans le plan, voir Singularités et Fonction zeta !