Comment
représenter une fonction complexe ?
Problématique
Soit
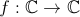 une fonction complexe. La question de vouloir la représenter
graphiquement se pose pour les gens qui aiment bien voir les choses
pour les comprendre (je ne suis pas le seul je pense). Pour
le
cas des fonctions
réelles, beaucoup de propriétés "topologiques" (de forme) peuvent être
visualisées
sur un graphe. On peut alors se demander dans quelle mesure on peut
créer une représentation des fonctions complexes conforme à quelques
propriétés topologiques des fonctions.
une fonction complexe. La question de vouloir la représenter
graphiquement se pose pour les gens qui aiment bien voir les choses
pour les comprendre (je ne suis pas le seul je pense). Pour
le
cas des fonctions
réelles, beaucoup de propriétés "topologiques" (de forme) peuvent être
visualisées
sur un graphe. On peut alors se demander dans quelle mesure on peut
créer une représentation des fonctions complexes conforme à quelques
propriétés topologiques des fonctions.1) Représentation des fonctions réelles
Pour les fonctions réelles, on a la chance que les écrans d'ordinateur et les feuilles de papier soient homéomorphes (et même isométriques) à une partie de
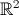 . Ainsi on met une dimension pour
l'argument et
une dimension pour le résultat de la fonction.
. Ainsi on met une dimension pour
l'argument et
une dimension pour le résultat de la fonction.Exemple pour la fonction
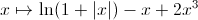 (tracée sur MAFA Traceur de courbes,
qui est bien pratique)
(tracée sur MAFA Traceur de courbes,
qui est bien pratique)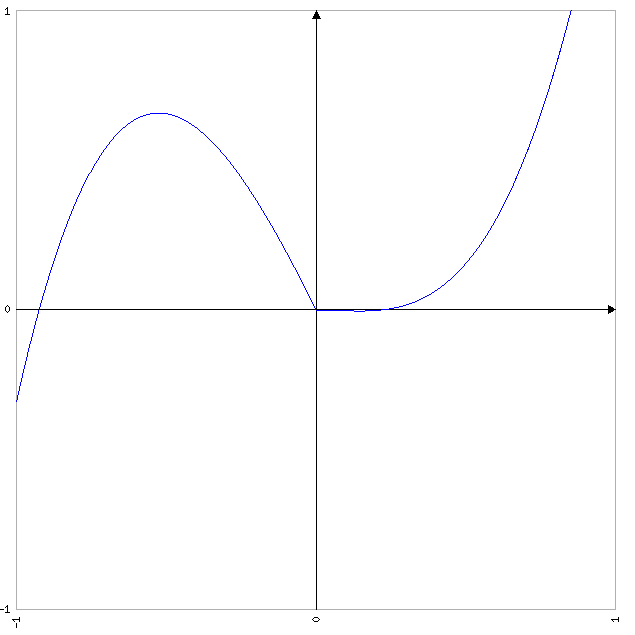
Le graphe nous informe de plusieurs propriétés : on peut y lire la continuité, la dérivabilité. Là on voit aussi que la fonction n'est pas dérivable en 0, on peut distinguer qu'elle est négative au voisinage de 0 à droite...
De façon générale, la représentation graphique permet d'illustrer :
- Le signe et les valeurs de la fonction tracée
- L'ensemble de définition
- Les intervalles de continuité, les points de discontinuité
- Le signe et les valeurs de la dérivée
- Le signe de la dérivée seconde
- Le signe de la dérivée troisième (sur certains exemples, en regardant très attentivement !)
...
Mais la représentation graphique (et cet exemple l'illustre) a de nombreuses failles évidemment :
- La limite de puissance informatique entraîne une limite de la finesse du tracé
- La taille étant bornée, on ne peut pas afficher le comportement à l'infini
- Certains "évenements" sont suffisament locaux pour n'être pas décelables sans les chercher : dans l'exemple tracé au dessus, on n'aurait pas vu que la fonction était localement négative à droite de 0 si on avait tracé un graphe plus global (sur un plus grand intervalle).
2) Représentations complexes
Il fallait donc trouver une façon de représenter les fonctions de
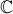 dans
dans 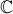 ,
qui à priori nécessite un espace ambiant de dimension 4. On
en a un sous la main : 3 dimensions spatiales et une dimension du
temps. Mais il serait difficile de lire des propriétés de fonctions sur
une surface 3D qui bouge en fonction du temps... (et il est encore plus
difficile probablement de construire un tel graphe)
,
qui à priori nécessite un espace ambiant de dimension 4. On
en a un sous la main : 3 dimensions spatiales et une dimension du
temps. Mais il serait difficile de lire des propriétés de fonctions sur
une surface 3D qui bouge en fonction du temps... (et il est encore plus
difficile probablement de construire un tel graphe)Le choix retenu est le suivant :
Les deux dimensions spatiales de l'écran servent à représenter le nombre où l'on évalue la fonction ;
L'image du point est représentée par une couleur.
Il faut savoir que l'ensemble des couleurs est homéomorphe à un cylindre ou un cube (en dimension 3) :
On peut décrire chaque couleur à l'aide de son code HSL (teinte, saturation, luminosité) ou de son code RGB (rouge vert bleu). Il s'agit donc de trouver une unique couleur à associer à chaque nombre complexe :
On choisit la représentation polaire du nombre :
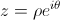 , et la représentation HSL des
couleurs
, et la représentation HSL des
couleursEn pratique : Avec le graphe de l'identité à droite, et la fenêtre gaphique à gauche :
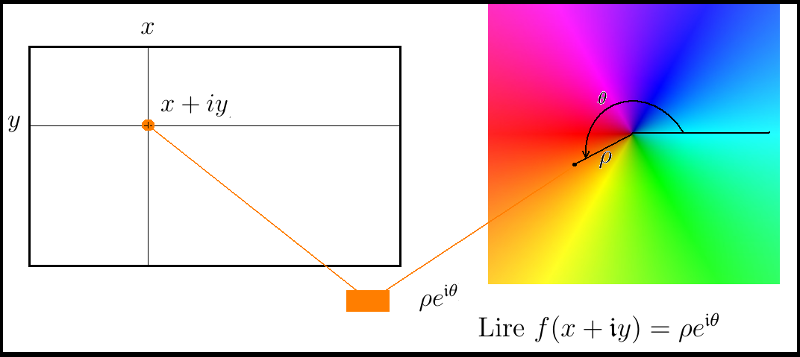
Si vous regardez au pixel ( x , y ), il faut comprendre qu'on va y lire f(x+iy) ;
Si vous y voyez la couleur orange, il faut se dire qu'elle décrit un unique nombre grâce à une bijection entre (une partie de) l'ensemble des couleurs et le plan complexe. Si la couleur correspond à
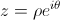 , alors z est
l'image du point (x,y) ou plutôt x+iy.
, alors z est
l'image du point (x,y) ou plutôt x+iy.On a une correspondance entre la représentation polaire, et la représentation HSL, la bijection se fait de la façon suivante :
- La saturation est fixée (on ne varie pas vers des nuances de gris)
- La teinte est proportionnelle à l'argument : par exemple le bleu clair décrit le réel positif
- La luminosité est proportionnelle au rayon (en fait, pas proportionnelle, le détail est juste après)
Alors on peut ainsi dessiner une fonction en coloriant les pixels d'un rectangle : l'argument de la fonction est la position sur l'écran, le résulat en ce point est la couleur renvoyée.
Voilà ce que ça donne pour
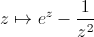 dessinée sur le
rectangle [-4,4] + i [-4,4]
dessinée sur le
rectangle [-4,4] + i [-4,4]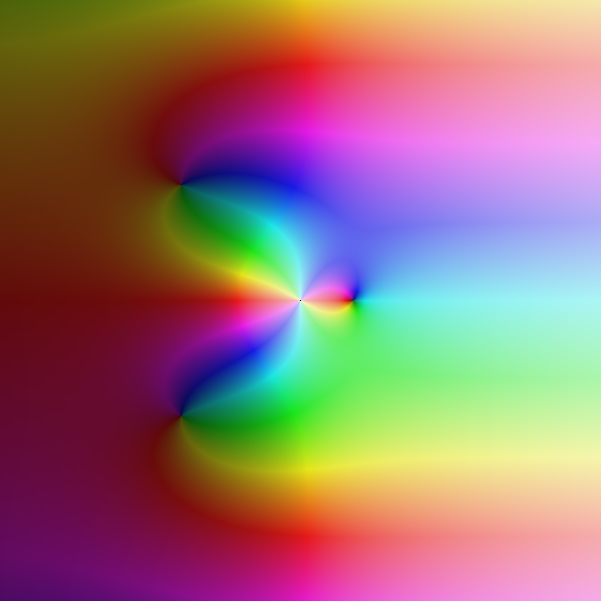
On l'a choisi ainsi car la teinte a la même "cyclicité" que l'argument : ils sont tous deux homéomorphes au cercle unité
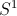 .
En mots plus simples, si l'on parcourt toutes les couleurs de la
teinte, on revient sur la couleur initiale ; de la même façon, en
parcourant tous les arguments possibles de -
.
En mots plus simples, si l'on parcourt toutes les couleurs de la
teinte, on revient sur la couleur initiale ; de la même façon, en
parcourant tous les arguments possibles de -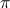 à
à 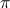 ,
on
peut identifier le départ à l'arrivée.
,
on
peut identifier le départ à l'arrivée.Ce qui est énorme, c'est que grâce à ça, la continuité est conservée par ce mode de représentation ... ou presque ! car en fait il n'y a pas de discontinuité de la couleur quand la fonction tend vers l'infini : Voir l'exemple ci-dessus : la fonction n'est pas définie en 0...
Malgré tout, de tels points sont très reconnaissables, ce qui rend cette contrainte moins grave.
Cette partie est adressée à un public familier de la topologie et des nombres complexes.
Vous pouvez passer directement à la partie 3 si ces sujets ne vous passionnent pas :)
En pratique, pour l'argument les choses se passent bien, car il est toujours borné et souvent facile à calculer. Pour le module, il faut prendre des précautions. Tout dépend toujours des valeurs des fonctions qu'on veut tracer. Si l'on trace une fonction continue sur un ensemble "petit", le module ne peut pas exploser et donc, pas de problème.
Mais si on trace une fonction qui a des zéros et des pôles, on a un problème : le zéro n'a aucune importance dans le tracé, le pôle englobe toute l'information (voir ci dessous à gauche).
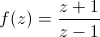 sur le carré [-2,2] + i [-2,2] :
sur le carré [-2,2] + i [-2,2] :
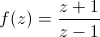 sur le carré [-2,2] +
i [-2,2] :
sur le carré [-2,2] +
i [-2,2] :

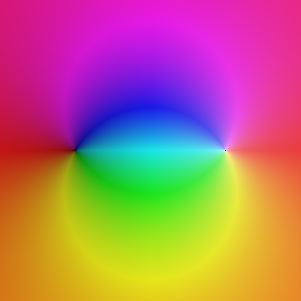
Sur la figure de gauche, on doit borner
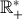 pour faire correspondre un MODULE à une LUMINOSITE. On choisit naïvement de définir
un nombre comme infini lorsqu'il dépasse un certain module (ici 10) donc "
pour faire correspondre un MODULE à une LUMINOSITE. On choisit naïvement de définir
un nombre comme infini lorsqu'il dépasse un certain module (ici 10) donc " 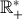 = [0,10] "
= [0,10] "Sur la figure de droite, on prend le logarithme du module, donc on fait la même opération pour borner Log(
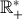 )=
)= 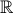 ;
; Ici on prend "
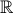 =[-3,3] " au sens où on considère que le module est nul s'il est inférieur à exp(-3), infini s'il est supérieur à exp(3).
=[-3,3] " au sens où on considère que le module est nul s'il est inférieur à exp(-3), infini s'il est supérieur à exp(3).Avec les deux illustration de la même fonction ci-dessus, on voit que l''idéal est de prendre le logarithme du module (voir la figure de droite) : ainsi la croissance à l'infini n'est pas trop brutale (donc on y voit quelque chose) et en plus, ça a l'avantage de donner la même importance aux zéros qu'aux pôles (quand on trace une fonction holomorphe ou méromorphe).
La figure de droite ne semble ici pas scandaleuse (bien que pas très belle) mais elle le devient pour d'autres exemples de fonctions :
En pratique, malgré la précaution du logarithme, les valeurs de
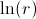 peuvent être
très variables (grandes). Il est donc préférable
de "compactifier"
peuvent être
très variables (grandes). Il est donc préférable
de "compactifier" 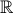 par exemple
avec
par exemple
avec 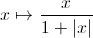 au lieu de
au lieu de 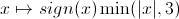 :
le nombre représentatif du module varie alors entre -1/2 et 1/2. Quand il
est proche de -1/2 on s'approche du module 0 ; quand il est proche de 1/2
on s'approche du module infini.
:
le nombre représentatif du module varie alors entre -1/2 et 1/2. Quand il
est proche de -1/2 on s'approche du module 0 ; quand il est proche de 1/2
on s'approche du module infini. Voici un exemple où cette précaution s'avère indispensable,
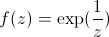 sur le carré [ -0.5 , 0.5 ] + i [ -0.5 , 0.5 ] :
sur le carré [ -0.5 , 0.5 ] + i [ -0.5 , 0.5 ] :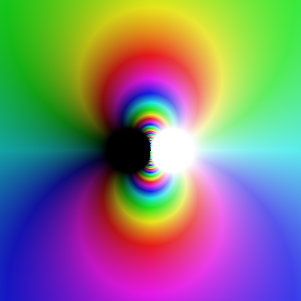

Là, les logarithmes sont tellement variables qu'il est indispensable de ne pas les borner stupidement, au risque de perdre beaucoup d'informations.
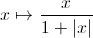 réalise un homéomorphisme entre la droite étendue de
réalise un homéomorphisme entre la droite étendue de 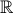 et [ -0.5 , 0.5 ] ainsi
on peut ainsi avoir une luminosité
représentative du module, et des images lisibles (et même belles
éventuellement !) comme le montre la figure de droite..
et [ -0.5 , 0.5 ] ainsi
on peut ainsi avoir une luminosité
représentative du module, et des images lisibles (et même belles
éventuellement !) comme le montre la figure de droite..Finalement, on trace une couleur correspondant au nombre complexe
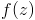 au pixel
correspondant au
complexe
au pixel
correspondant au
complexe  .
.
La teinte (entre -
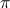 et
et 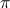 )
vaut
)
vaut 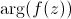 et la
luminosité (entre
-1/2 et
1/2) vaut
et la
luminosité (entre
-1/2 et
1/2) vaut 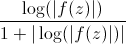
3 )Comment lire les valeurs de la fonction ?
Pour lire les valeurs de la fonction, il faut avoir en tête la dégaine de l'identité. Une fois qu'on a bien en tête la correspondance entre les couleurs et les nombres, il est facile d'imaginer le comportement d'une fonction en voyant son graphe.
Graphe de
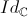 sur le carré [-10,10] + i [-10,10] :
sur le carré [-10,10] + i [-10,10] :![Identité Identité sur [-10,10]+i[-10,10]](documents/Id.png)
4) Premières propriétés
Comme on l'a vu, les points particuliers apparaîssant les plus clairement sont les zéros (en noir) et les pôles (en blanc). Ils apparaîssent avec la même "importance" grâce à la manoeuvre du logarithme.
Les points d'image réelle sont représentés en bleu clair (cyan) ou en rouge selon le signe.
Les points d'image imaginaire pure sont bleu-violets ou vert-jaunes.
Tout ça est assez imprécis mais ça donne quand même une idée du comportement d'une fonction.
Cette représentation est assez conforme aux ambitions qu'on lui vouait initialement : elle rend visible des propriétés de la fonction comme : la continuité, l'ensemble de définition, les points d'annulation, les multiplicités des pôles ou des zéros, les points d'annulation de la dérivée (c'est pas rien quand même !) , parfois on peut voir des sous ensembles stables, des périodicités, les propriétés d'une singularité....
Elle a tout de même des défauts : comme pour les représentations réelles, on ne peut à priori pas dessiner l'image d'une fonction sur
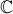 tout entier. C'est en
fait
possible mais j'en parlerai pas ici. On en parle sur la page Homographies !
tout entier. C'est en
fait
possible mais j'en parlerai pas ici. On en parle sur la page Homographies ! Un autre problème est le manque de compatibilité avec la somme : avec la donnée de deux graphes de fonctions f et g tracés, il est très difficile et contre-intuitif d'anticiper la forme du graphe de f + g. En revanche la forme de fg est quant à elle assez limpide : les zéros et les pôles sont les mêmes, et les teintes s'ajoutent. Cette compatibilité avec le produit et non la somme vient (à méditer) de ce même fait pour la représentation polaire de deux nombres complexes.
Illustration de ce phénomène :
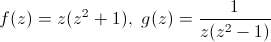


f g


fg f+g
Et là, on voit que la somme est non congruente. Ce serait encore plus visible avec des fonctions prenant toutes les deux de grandes valeurs (et assez différentes pour les deux fonctions).
Pour aller un peu plus loin pour comprendre les fonctions et leurs représentations, voir la page Lecture des graphes !
Sinon, pour voir plusieurs exemples connus de graphes, RDV sur la page Fonctions principales !