1) Exploration d'un germe

   Pour Bob, si la notion de germe de fonction analytique lui est étrangère, j'ai essayé de proposer une illustration du prolongement d'un germe. Prolonger un germe, c'est comme avancer dans une obscurité qui s'éclaire sur son passage (de façon permanente).
Un germe de fonction analytique est la donnée d'un point, et d'un série entière de rayon de convergence strictement positif. On choisit un voisinage de convergence sur lequel on "éclaire" la fonction, et on la prolonge de proche en proche là où c'est possible. Le prolongement local est unique par le théorème de prolongement analytique. On crée comme ça une fonction.
   Ainsi, les valeurs d'une fonction provenant du prolongement d'un germe ne dépendent que du chemi suivi pour atteindre les points.

On a un germe de fonction analytique au point 1 : c'est le germe du  Log principal  sur le carré [-4,4] + i [-4,4] :
                                
     
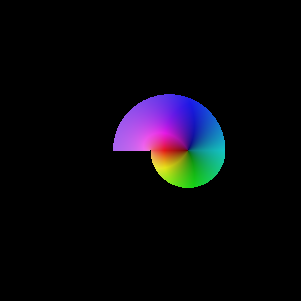
Le prolonger revient à exprimer la seule fonction analytique coïncidant de proche en proche sur l'ouvert où on l'a éclairée. On peut le prolonger où on veut sauf en 0. Comme il s'agit du logarithme, la fonction peut être définie comme intégrale de 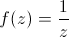  le long d'une courbe choisie (pour une preuve mathématique), ou avec une définition localement continue de l'argument (pour le calcul informatique). Pour plus de détails sur la méthode, voir "rotation du logarithme" sur Déterminations !
  Comme 0 est l'unique singularité intrinsèque de ce germe, on va le prolonger en tournant autour de 0 :
On le prolonge en suivant une courbe d'arguments croissants comme ça :
     Sur le disque D(  1/2   ,  1-1/2  ), y<0  -  sur le disque D(1,2), y>0
     Sur le disque D(  1/2   ,  2-1/2  ), y<0  -  sur le disque D(1,3), y>0
     Sur le disque D(  1/2   ,  K-1/2  ), y<0  -  sur le disque D(1,K), y>0 :

                             
                   
         On voit maintenant les discontinuités (inhabituelles) du logarithme apparaître.  Voici un cas où on ne peut pas recoller le germe de l'autre côté de la singularité. En fait, le germe de départ est prolongeable le long de tout chemin de , qui n'est pas convexe ou étoilé  (ni simplement connexe) et c'est pour ça qu'on ne peut pas prolonger le logarithme à .

    C'est le théorème de monodromie qui permet d'affirmer que si U est convexe ou étoilé, et qu'on prend un germe G prolongeable le long de tout chemin de U, il existe une fonction analytique sur U dont G est un germe.

 En revanche, cette condition n'est pas nécessaire. Dans la suite, un exemple où on peut prolonger un germe de façon analytique sur .


2) Séries entières et fonctions analytiques

   Il est raisonnable de se demander dans quelle mesure on peut prolonger un germe de fonction analytique : cela revient à se demander sur quel "ensemble maximal" une série entière donnée peut définir une fonction. Un exemple aussi présent dans Homographies présente une série entière non prolongeable au delà du disque de convergence :  
                     
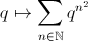
            Cette série entière (une série lacunaire) ne se prolonge pas au delà du disque. Elle a des discontinuités denses dans le cercle.
Pour voir d'autres fonctions ressemblantes (et pas de façon fortuite) RDV sur Fonctions modulaires !
Mais ici on va plutôt s'intéresser aux séries entières qu'on peut prolonger dans certaines directions. Par exemple .


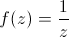On choisit un germe de f  : au point 2 (figure de droite) , la série de Taylor donne le germe de f.  Ce germe (comme celui du logarithme précédemment) est prolongeable partout sauf en 0.
   On peut la prolonger de proche en proche à l'aide des séries entières tant qu'on évite 0 :
                                     

    Sur l'image de gauche on voit bien que les germes se rejoignent de l'autre côté de la singularité sans être différents pour autant. Ce résultat était (plus que) très prévisible : on connaît une fonction analytique définie (globalement) sur qui coïncide avec le germe de départ sur une boule, est connexe, donc ils coïncident sur .
     Si Bob n'a pas saisi la différence avec le logarithme, il doit prendre conscience que dans le cas décrit ici, on a déjà une expression de notre germe, qu'on sait holomorphe sur . C'est différent du logarithme, qui est défini par une intégrale donc sa définition est uniquement locale. Pour le logarithme, rien ne permet d'avoir une définition globale sans prolonger de proche en proche.

    Le prolongement d'une série de Dirichlet hors de son demi-plan de définition n'est pas un problème simple non plus. On peut assimiler ces deux problèmes par homographies, les résultats sont donc transcriptibles de l'un à l'autre. Pour une illustration du prolongement de, pas une, mais 2 fonctions avec des demi-plans de convergence, allez voir Fonction zeta !
   Pour voir d'autres fonctions non prolongeables au delà d'un disque ou demi plan, RDV sur Fonctions modulaires.


3) Développement en séries entières

   On se propose d"étudier la série suivante :   Une étude rapide donne un rayon de convergence 1. Voici un tracé des sommes partielles sur [ -1.5 , 1.5 ] + i [ -1.5 , 1.5 ] aux rangs 4 et 14 :
                                     

      On voit un comportement se profiler pour la limite au milieu du disque. Les zéros des polynômes sont presque tous envoyés vers le cercle de frontière, et une divergence grossière se prépare à l'extérieur du disque. Si on continue plus loin dans la somme, tous ces comportements s'accentuent encore :
                                 

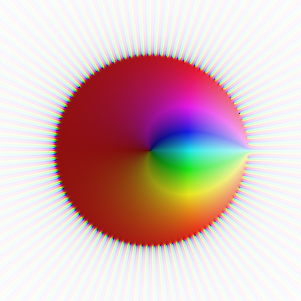
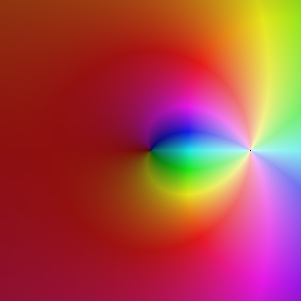
   À gauche on a tracé la somme partielle au rang 100, on peut commencer à distinguer qu'en fait, un seul point du cercle pose problème pour prolonger la série hors du cercle. Cela est difficile à vérifier : pour savoir qu'on peut prolonger la fonction en un point a, il faut à priori vérifier que la limite est bornée sur : 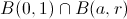pour un certain r positif. Parfois on a une convergence ponctuelle de la série au point a, mais ce n'est pas nécessaire (voir exemple ci-dessus), ni suffisant (voir l'exemple de ).

   Par contre quoi qu'il arrive, la série entière de départ n'est plus valide pour approcher la fonction. En pratique, on peut regarder le rayon de convergence de la série entière translatée en chaque point du disque, et voir lesquels permettent de "s'échapper du disque". Mais pour l'exemple que j'ai donné, on peut exprimer la fonction sur 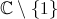: c'est 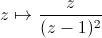. On peut prouver que les deux fonctions coïncident sur B(0,1), donc sur 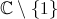 par connexité. La fonction est tracée à droite, et il est bien clair que la série entière ne peut plus la décrire hors du disque de convergence. Ce n'est que le cas pour les fonctions entières, là les séries décrivent les fonctions sur tout entier, ce qui leur donne de belles propriétés (théorème de Picard, par exemple :)
Pour voir d'autres germes de fonctions analytique, RDV sur Déterminations !