1) Fonctions périodiques
Dans cette section on tracera les graphes sur les pavés [-7,7] + i [-7,7].
La fonction exponentielle :

On voit que les réels sont envoyés sur les réels positifs (ligne bleue horizontale au milieu). De plus le module augmente quand la partie réelle des points évalués augmente (en direction de la droite), donc le graphe s'éclaircit de gauche à droite. Enfin, on voit un période imaginaire pure : le graphe se répète en le déplaçant de 2i
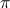 (vers le haut ou vers
le
bas).
(vers le haut ou vers
le
bas).La fonction sinus :

Celle ci a une période de 2
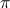 ,
donc le graphe se répète lors des déplacements horizontaux. On voit sin(0)=0. Par
ailleurs le module croît (de façon exponentielle) losque la partie
imaginaire est grande.
,
donc le graphe se répète lors des déplacements horizontaux. On voit sin(0)=0. Par
ailleurs le module croît (de façon exponentielle) losque la partie
imaginaire est grande.La fonction cosinus : sur sur [-2
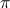 ,2
,2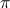 ]
+ i [-2
]
+ i [-2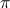 ,2
,2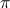 ]
La fonction tangente
sur [-2
]
La fonction tangente
sur [-2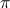 ,2
,2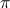 ] + i [-2
] + i [-2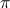 ,2
,2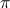 ]
]

Le cosinus ressemble beaucoup au sinus à cause de la formule
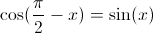 . Un déplacement du
plan
envoie le graphe du sinus sur celui du cosinus.La période réelle de la
tangente est deux fois plus courte :
c'est
. Un déplacement du
plan
envoie le graphe du sinus sur celui du cosinus.La période réelle de la
tangente est deux fois plus courte :
c'est 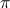 .
Elle alterne les pôles et zéros sur l'axe réel, stabilise le demi-plan
de Poincarré, et n'a pas de branche infinie (au sens où il n'y a aucune
direction sur laquelle le module tend vers l'infini). La fonction
tangente est méromorphe, car c'est le quotient de deux fonctions
holomorphes.
.
Elle alterne les pôles et zéros sur l'axe réel, stabilise le demi-plan
de Poincarré, et n'a pas de branche infinie (au sens où il n'y a aucune
direction sur laquelle le module tend vers l'infini). La fonction
tangente est méromorphe, car c'est le quotient de deux fonctions
holomorphes.2) Fonctions réciproques
Il est bon de noter que le fonctions admettant une réciproque holomorphe sont rares. Par exemple les uniques fonctions holomorphes sur
 et bijectives sont les fonctions affines. Pour inverser une fonction
entière, on doit choisir une restriction de
et bijectives sont les fonctions affines. Pour inverser une fonction
entière, on doit choisir une restriction de 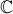 sur laquelle la fonction est injective, puis l'inverser. La plupart du
temps les fonctions trouvées sont multiformes. Dire que f est mutiforme signifie qu'il existe une autre fonction g coïncidant avec f sur un ouvert, et que sur un autre ouvert f et g sont distinctes.
sur laquelle la fonction est injective, puis l'inverser. La plupart du
temps les fonctions trouvées sont multiformes. Dire que f est mutiforme signifie qu'il existe une autre fonction g coïncidant avec f sur un ouvert, et que sur un autre ouvert f et g sont distinctes.On commence par le logarithme, il va servir pour toutes les autres :
Fonction logarithme sur [-2,2] + i [-2,2]
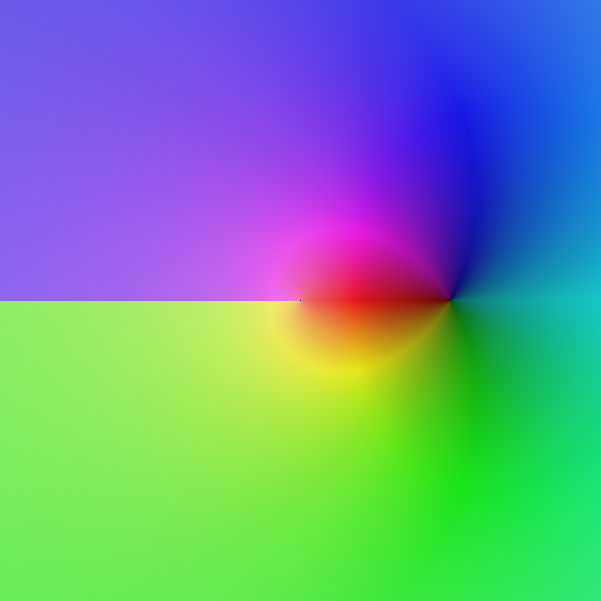
C'est la version la plus couramment utilisée du logarithme : le logarithme principal.
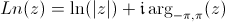 Il amène des
déterminations des racines n-ièmes, qui
dépendent du choix d'un logarithme, et du choix de quelle racine on a
l'intention de prendre :
Il amène des
déterminations des racines n-ièmes, qui
dépendent du choix d'un logarithme, et du choix de quelle racine on a
l'intention de prendre :Disons qu'on a choisi un logarithme ; une fonction
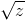 est donnée
par
est donnée
par 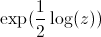 ou
ou 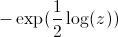 .
On a donc le
choix
entre deux déterminations de la
racine à logarithme fixé. De la même façon (expliqué juste après) un
choix de logarithme et de racine carrée détermine un arc-sinus :
.
On a donc le
choix
entre deux déterminations de la
racine à logarithme fixé. De la même façon (expliqué juste après) un
choix de logarithme et de racine carrée détermine un arc-sinus :Fonction racine
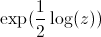 sur [-2,2] + i [-2,2] :
Fonction
arc-sinus sur [-2,2] + i [-2,2]
sur [-2,2] + i [-2,2] :
Fonction
arc-sinus sur [-2,2] + i [-2,2]

À gauche, on a choisi une des deux racines venant de notre logarithme. On peut noter qu'elle ne prend que la moitié des valeurs du plan : les arguments qu'elle peut atteindre sont définis par le choix des déteminations. Par ailleurs, l'opposée balaie toutes les couleurs manquantes sur ce graphe. Pour en voir beaucoup plus sur les racines et logarithmes, RDV sur Déterminations !
Pour la fonction arc-sinus : en écrivant tout comme si les racines et logarithmes étaient bien définis (la version avec les mains), on résoud l'équation
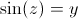 et
on trace
et
on trace 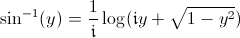 Comme
on a déjà déterminé une fonction
racine et une fonction
logarithme, on a déterminé un arc-sinus. On voit qu'au
voisinage de 0 elle ressemble à l'identité (tout comme
sinus). Elle a deux demi-droites de discontinuité, qui partent
respectivement de -1 et 1. Pour revoir l'arc-sinus comme vous ne l'avez
jamais vu, rendez vous sur Déterminations
aussi !
Comme
on a déjà déterminé une fonction
racine et une fonction
logarithme, on a déterminé un arc-sinus. On voit qu'au
voisinage de 0 elle ressemble à l'identité (tout comme
sinus). Elle a deux demi-droites de discontinuité, qui partent
respectivement de -1 et 1. Pour revoir l'arc-sinus comme vous ne l'avez
jamais vu, rendez vous sur Déterminations
aussi !De la même façon
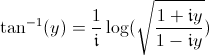 avec des choix de déterminations supposés connus.
avec des choix de déterminations supposés connus.Fonction arc-tangente :

Elle aussi ressemble à l'identité au voisinage de 0. Les discontinuités sont les deux demi-droites imaginaires pures partant de i et de -i. Celle ci aussi dépend des déterminations. Pour ces deux fonctions (comme la plupart du temps) j'ai choisi la détermination principale du log et la première racine carrée.
Toutes les fonctions qu'on a dessinées ici sont les déterminations principales de log, racine, arc-sin, arc-tan. Elles n'ont rien de particulièrement intrinsèques, mais elles ont toutes le mérite de prolonger celles qu'on connaît sur
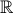 (enfin, sur les sous parties de
(enfin, sur les sous parties de 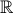 où elles sont définies). Sur la page Déterminations on peut voir des logarithmes ne prolongeant pas celui de
où elles sont définies). Sur la page Déterminations on peut voir des logarithmes ne prolongeant pas celui de 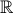 .
.3) Monômes et fractions rationnelles
On a déjà rencontré quelques monômes, en voici d'autres :
La fonction cube
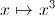 sur [-2,2] + i [-2,2] :
L'inverse
au
carré :
sur [-2,2] + i [-2,2] :
L'inverse
au
carré : 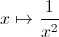 sur [-2,2] + i [-2,2] :
sur [-2,2] + i [-2,2] : 

Le zéro étant triple (à gauche), l'argument fait 3 tours autour de 0. On voit que la droite réelle est stable. Pour le pôle, on voit de même son ordre 2 au fait que l'argument fait 2 tours. Les monômes se ressemblent car tous les monômes stabilisent l'ensemble des cercles centrés en 0.
Voyons maitenant un polynôme
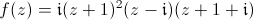 :
sur [ -1.5 , 1.5 ] + i [ -1.5 , 1.5 ]
:
sur [ -1.5 , 1.5 ] + i [ -1.5 , 1.5 ]
On a un zéro double et deux zéros simples, la fonction s'échappe à l'infini dans toutes les directions. Elle a un pôle d'ordre 4 à l'infini, c'est le degré du polynôme. Pour voir un pôle de polynôme à l'infini, RDV sur Homographies !
Une fraction rationnelle : homographie
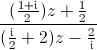 :
:
Il est intéressant de noter que les lignes d'équimodules et les lignes de mêmes arguments (modulo
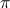 ) sont des cercles ou des droites. Les
homographies envoient les cercles-droites vers des cercles-droites...
) sont des cercles ou des droites. Les
homographies envoient les cercles-droites vers des cercles-droites...4) D'autres fonctions...
Avec tout ça on peut déjà imaginer quelques fonctions plus complexes mais encore simples. Genre les facteurs de Weierstrass, qui permettent de donner l'existence d'une fonction entière s'annulant sur S, pour tout S ensemble de points isolés.
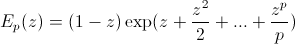 définit une
fonction entière qui ne s'annule qu'en 1.
définit une
fonction entière qui ne s'annule qu'en 1.En voilà un avec p=3, sur le carré [-3,3] + i [-3,3] :

On peut même regarder sa singularité à l'infini (de plus près, [ -0.5 , 1.5 ] + i [-1,1]) :

Trois belles branches infinies dues à un terme en X^3 qui devient le plus balaise au voisinage de l'infini. Il se trouve que cette fonction est d'ordre 3. Cependant toutes les singularités de fonctions d'ordre i n'ont pas cette dégaine...
Pour s'en convaincre, la singularité du sinus (d'ordre 1) est sur la page Singularités !
D'autres singularités à l'infini et ramenées dans le plan sont éparpillées sur plusieurs pages...
Une petite dernière, quelle est la forme de
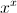 ?
sur [-3,3] + i [-3,3]
?
sur [-3,3] + i [-3,3] 
La demi droite de discontinuité vient du fait que
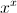 =exp(x.Log(x))
Donc le logarithme étant discontinu, lui aussi est disontinu. On voit
par ailleurs que la direction des réels positifs voit une forte
croissance de la fonction.
=exp(x.Log(x))
Donc le logarithme étant discontinu, lui aussi est disontinu. On voit
par ailleurs que la direction des réels positifs voit une forte
croissance de la fonction.Si Bob observe attentivement la droite de discontinuité, il verra peut-être qu'elle a des points de continuité sur les entiers négatifs : quand la couleur est rouge ou bleue (car c'est aussi l'ensemble des points d'image réelle sur la discontinuité) on peut traverser la droite sans changement brusque de couleur.
On a à peu près fait le tour des fonctions classiques, il y a d'autres sections pour voir des fonctions peut-être un peu plus exotiques !